Notes
square on an octagon solution
Solution to the Square on an Octagon Puzzle
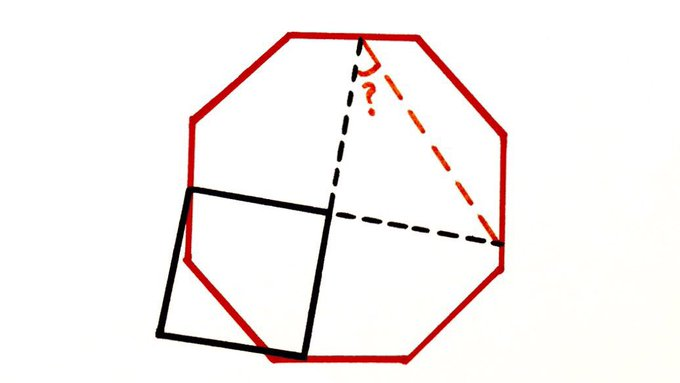
Two of the square’s corners lie on the regular octagon. What’s the angle?
Solution by Symmetry and Isosceles Right-Angled Triangle
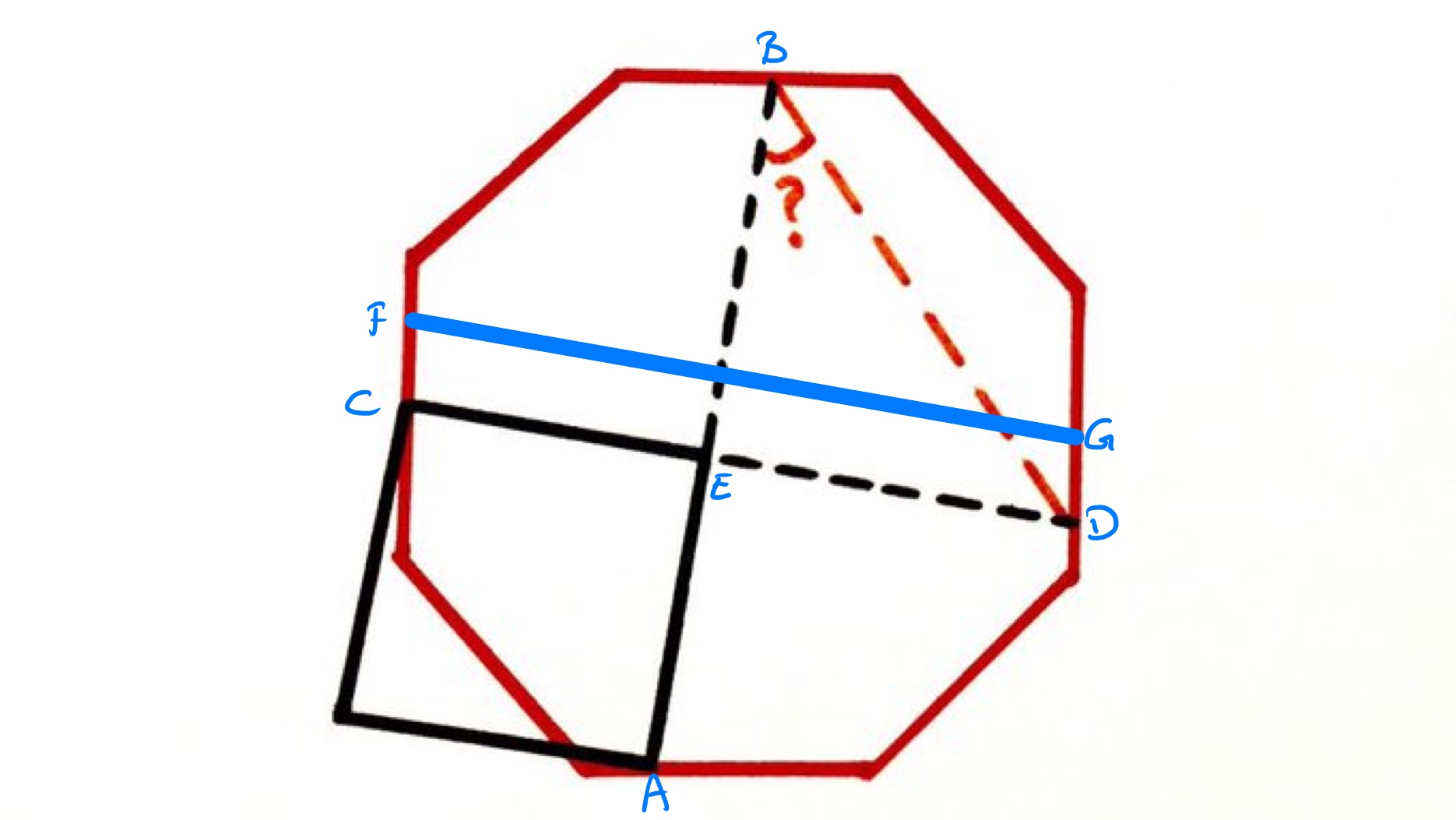
In the above diagram, the line segment is the rotation of about the centre of the octagon. It therefore has the same length as . The line segment is parallel to since it also intersects at right-angles. As both and end on the same sides of the octagon, they are the same length. So is the same length as . Since and are sides of the square, they have the same length and hence and have the same length. Therefore is an isosceles right-angled triangle and so angle is .