Notes
square in a triangle in a square solution
Solution to the Square in a Triangle in a Square Puzzle
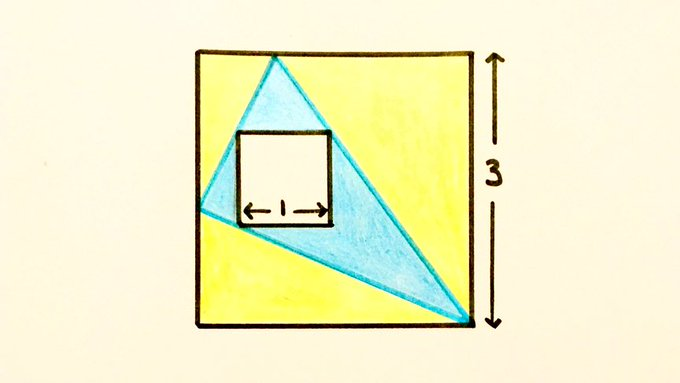
The sides of the two squares are parallel to each other. What’s the ratio of the blue area to the yellow?
Solution by Dissection and Area of a Triangle
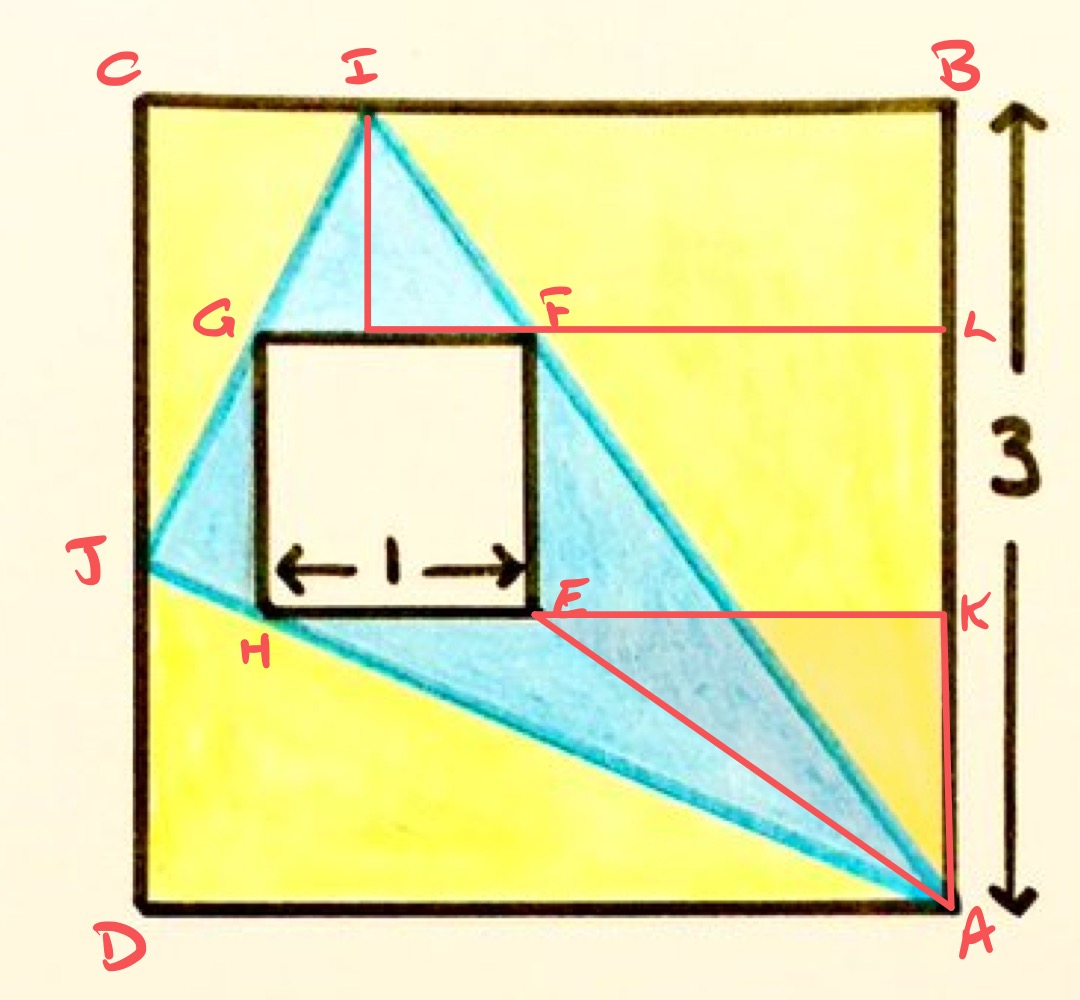
Consider the diagram as labelled above. The line from to means that the blue region consists of four triangles, each of which can be thought of as having a base along one of the edges of the inner square.
The vertical height of above is the same as the length of . Similarly, the vertical height of to is the same as the length of . The length of is that of the side of the inner square, so the sum of the lengths of and is . This means that the sum of the areas of and is .
A similar argument says that the areas of the other two blue triangles also sum to . So the total area of the blue regions is .
The yellow region therefore has area . So the ratio of the blue area to the yellow is .
Solution by Invariance Principle
There is a range of positions for the small square within the larger square, and at one extreme is the configuration below where it is in the middle against the left-hand edge.
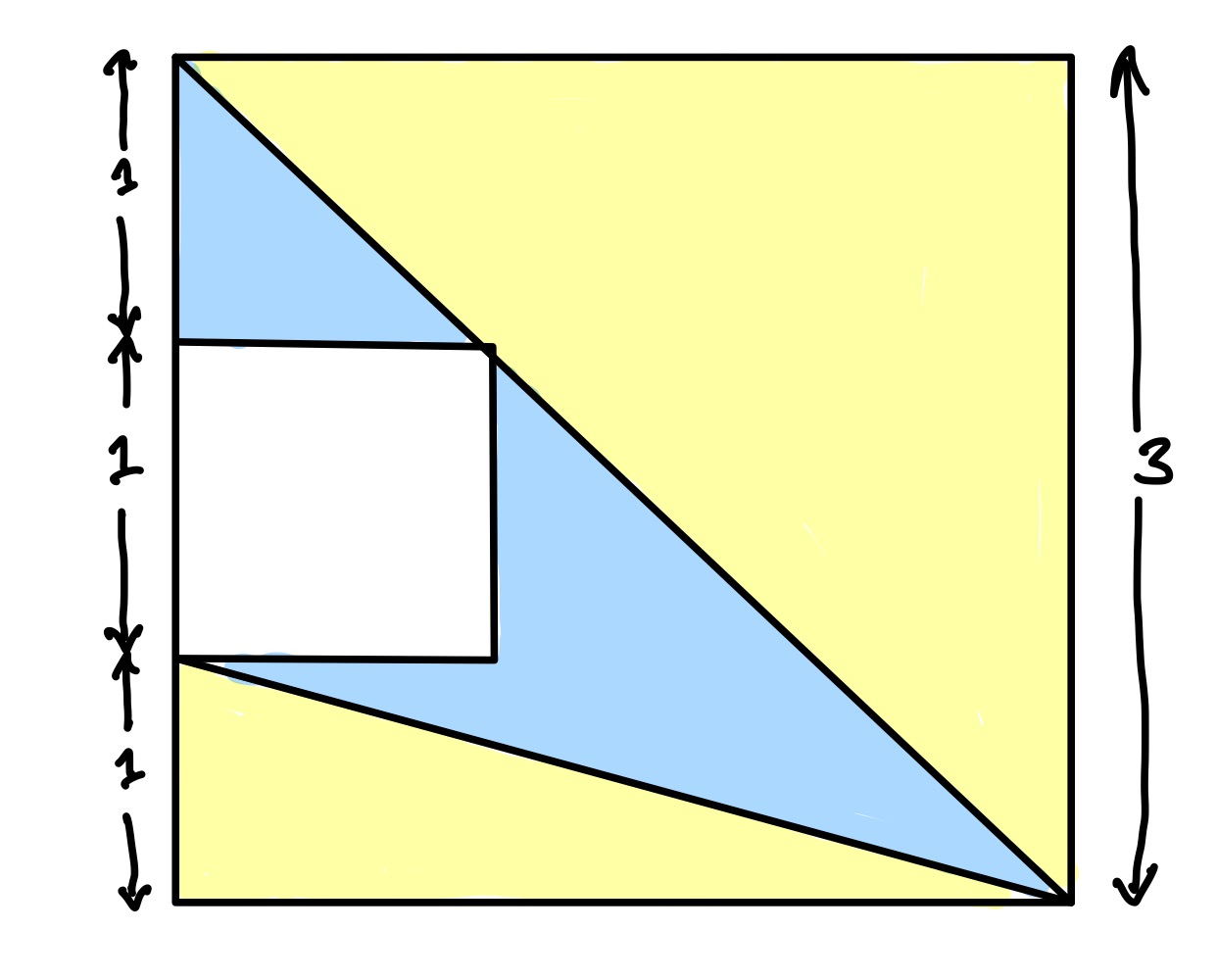
In this configuration, the top right corner of the small square lies on the diagonal of the outer square.
The large yellow triangle has area . The smaller yellow triangle has area . So the yellow area is .
The total area of the square is , so the total blue region has area .
Therefore the ratio of the blue area to the yellow is .