Notes
square in a semi-circle in a square solution
Square in a Semi-Circle in a Square
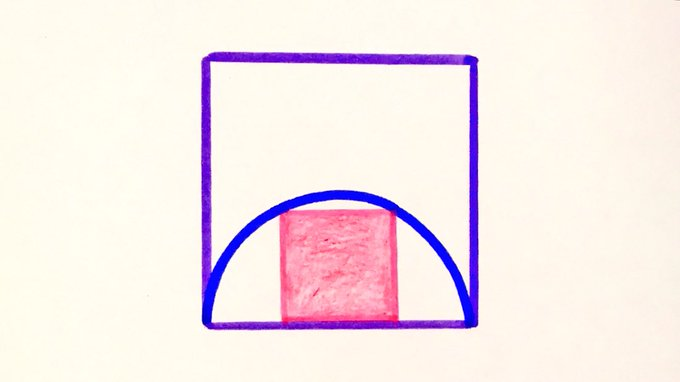
What fraction of the larger square is covered by the one inside the semicircle?
Solution by Properties of Chords and Pythagoras' Theorem
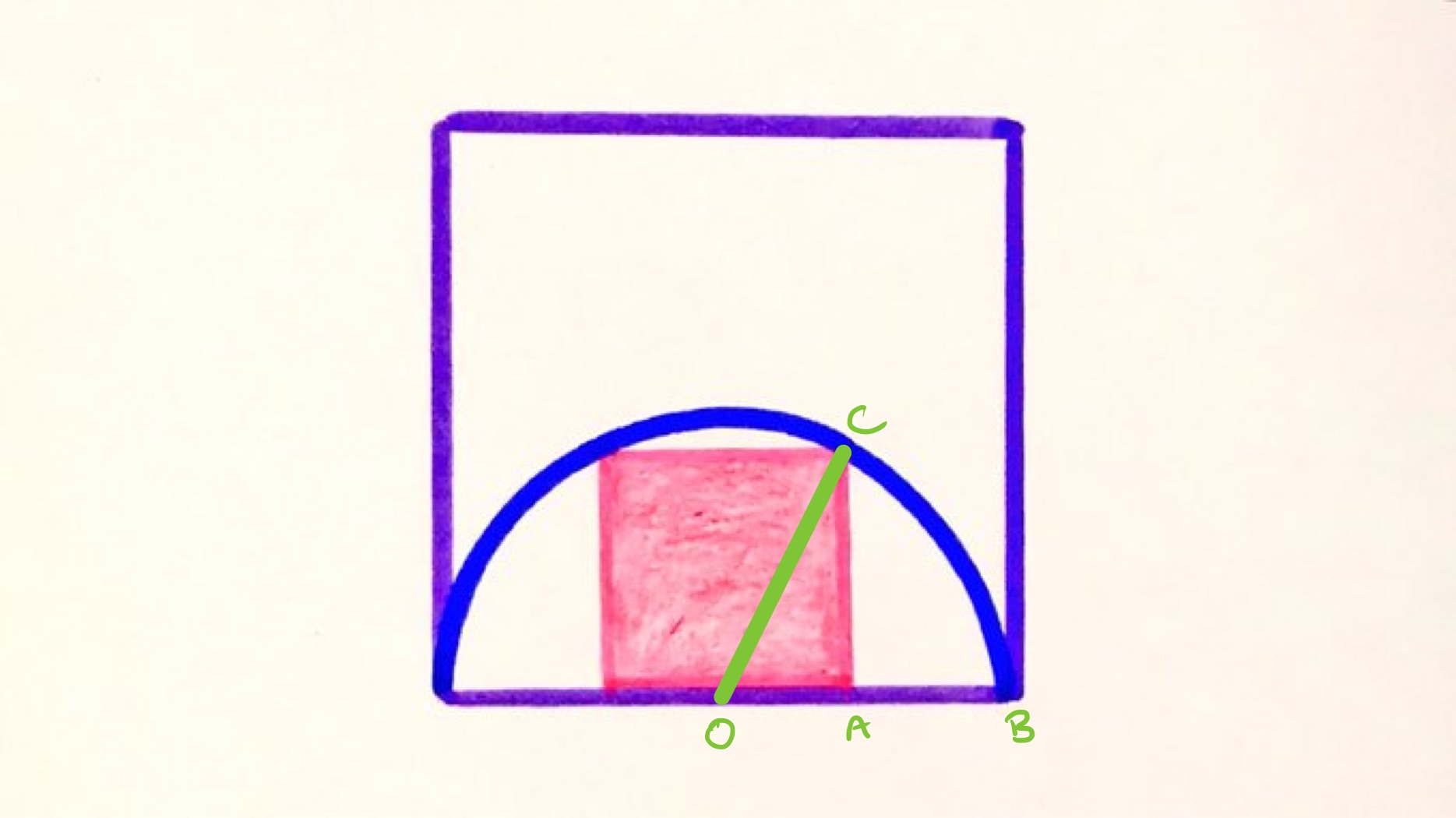
Since the top edge of the smaller square is a chord of the semi-circle, the centre of the circle lies on its perpendicular bisector and so is the midpoint of the bottom edge. This means that, in the above diagram, the length of is half that of . Writing for the length of , this means that is . The area of the smaller square is then .
Let be the length of . Since is a right-angled triangle, applying Pythagoras' theorem shows that . As has the same length as , the area of the outer square is then . The outer square is therefore times bigger than the smaller, and so the fraction that is shaded is th.