Notes
square in a circle in a quarter circle in a square solution
Square in a Circle in a Quarter Circle in a Square
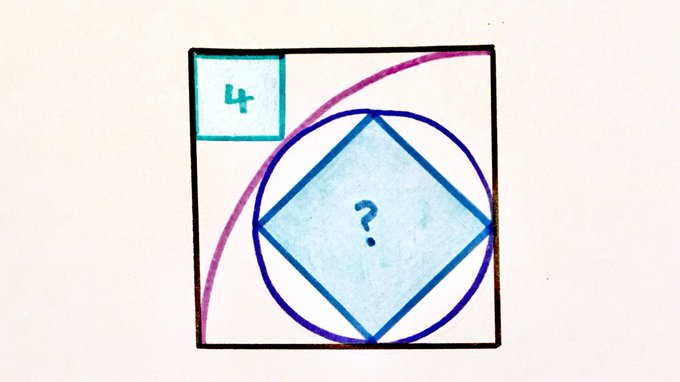
There are three squares here. The smallest has area . What’s the missing area?
Solution by Properties of Squares
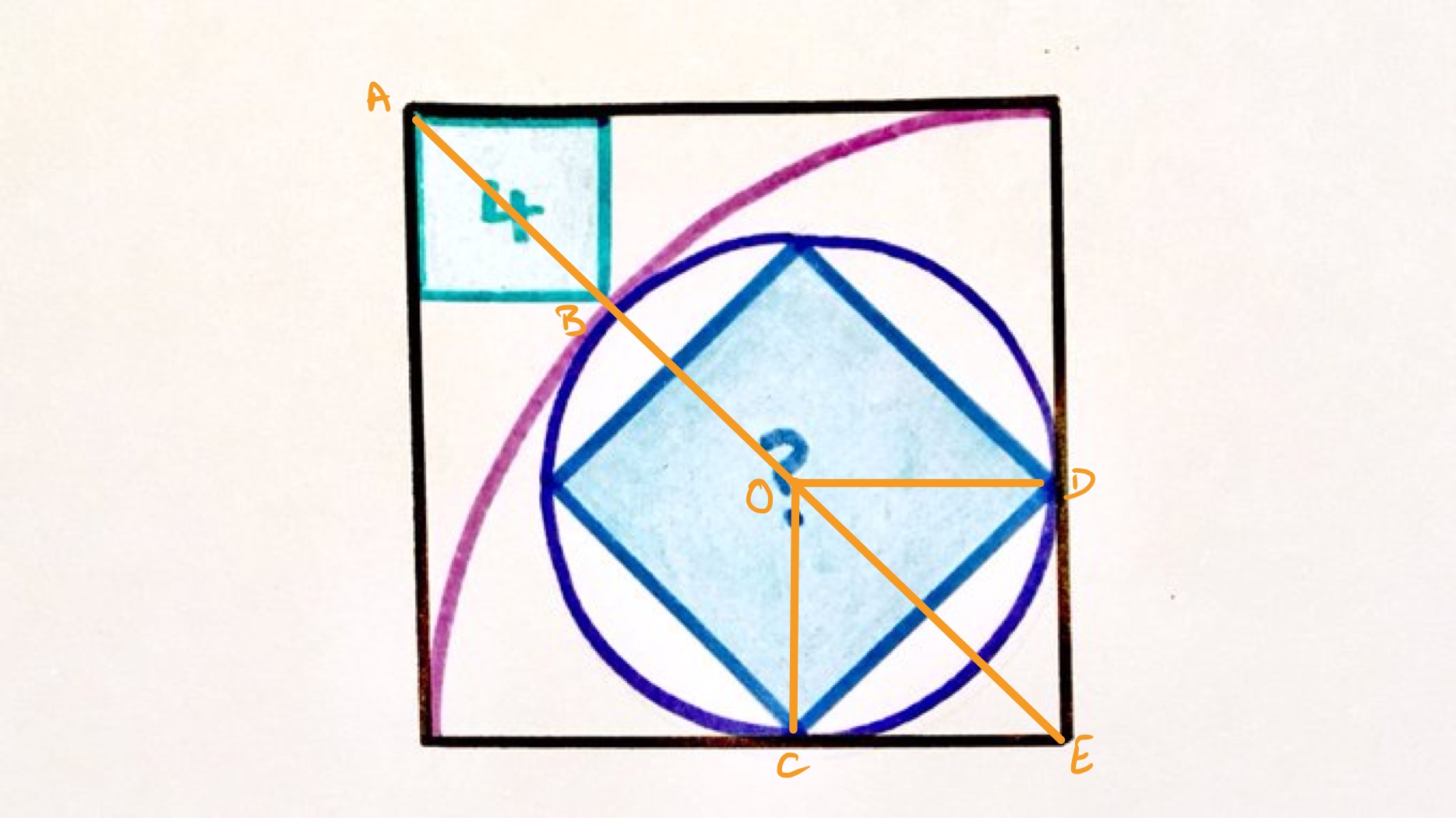
In the above diagram, let , , and be the side lengths of the three squares in ascending order. As the smallest square has area , its side length is so . The line segment is a diagonal of the smallest square so its length is .
The diagonal of the outer square has length . The radius of the quarter circle is , so the length of is and then of is . Putting these together shows that so .
The length of is the same as that of , which is as it is half a diagonal of the middle square. This then shows that has length since it is the diagonal of a square with side length . So has length . As this is the same as , this gives the following expression for :
Hence the area of the middle square is .