Notes
square and rectangle overlapping in a semi-circle solution
Square and Rectangle Overlapping in a Semi-Circle
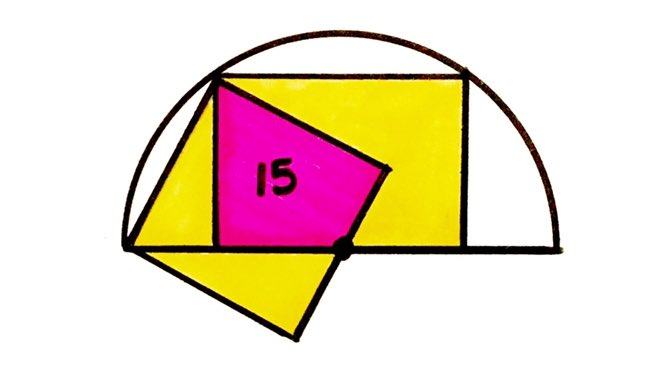
The square and rectangle intersect at the centre of the semicircle. What’s the total yellow area?
Solution by Area of a Triangle and Congruent Triangle
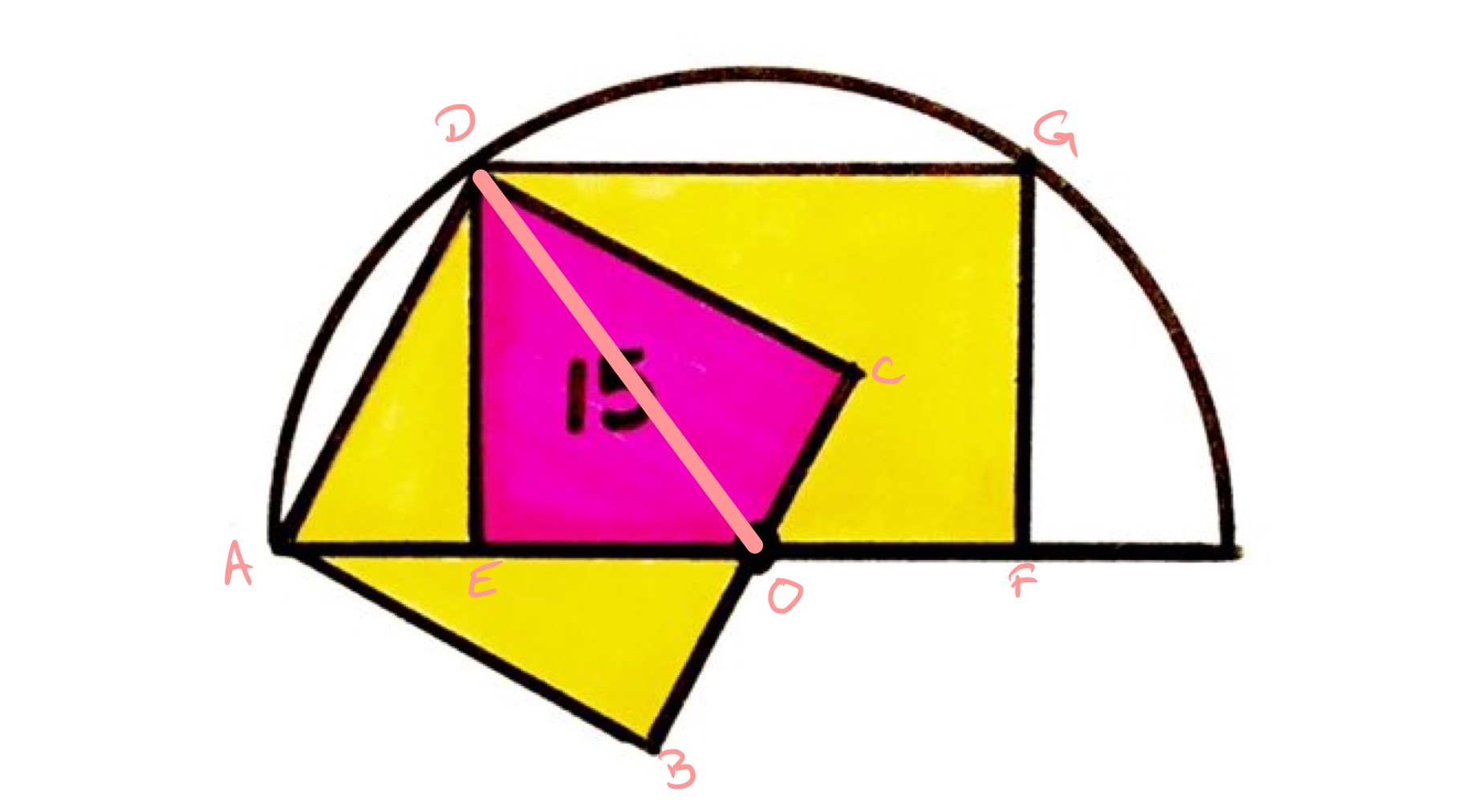
With the points labelled as above, both and are radii of the semi-circle and so have the same length. Triangle is therefore isosceles and so triangles and are congruent. This means that is half the length of and so the area of triangle is a quarter of that of the whole square.
A similar argument applies to rectangle to show that the area of triangle is a quarter of that of the whole rectangle.
The two rectangles taken separately (that is, without considering their overlap) is therefore . To find the area of the yellow regions, each then needs the purple region removed so the area of the yellow region is .