Notes
six triangles in a hexagon solution
Solution to the Six Triangles in a Hexagon Puzzle
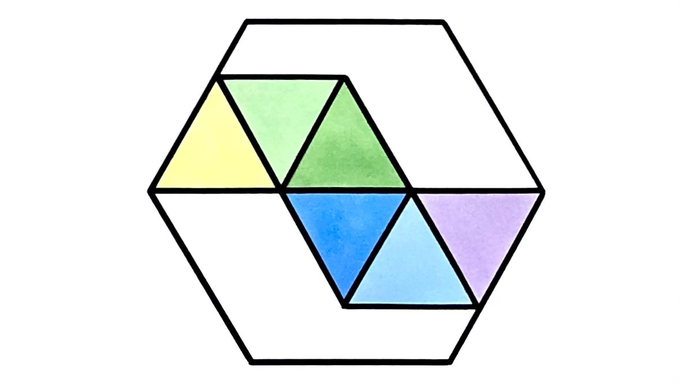
What fraction of this regular hexagon do the equilateral triangles cover?
Solution using Area
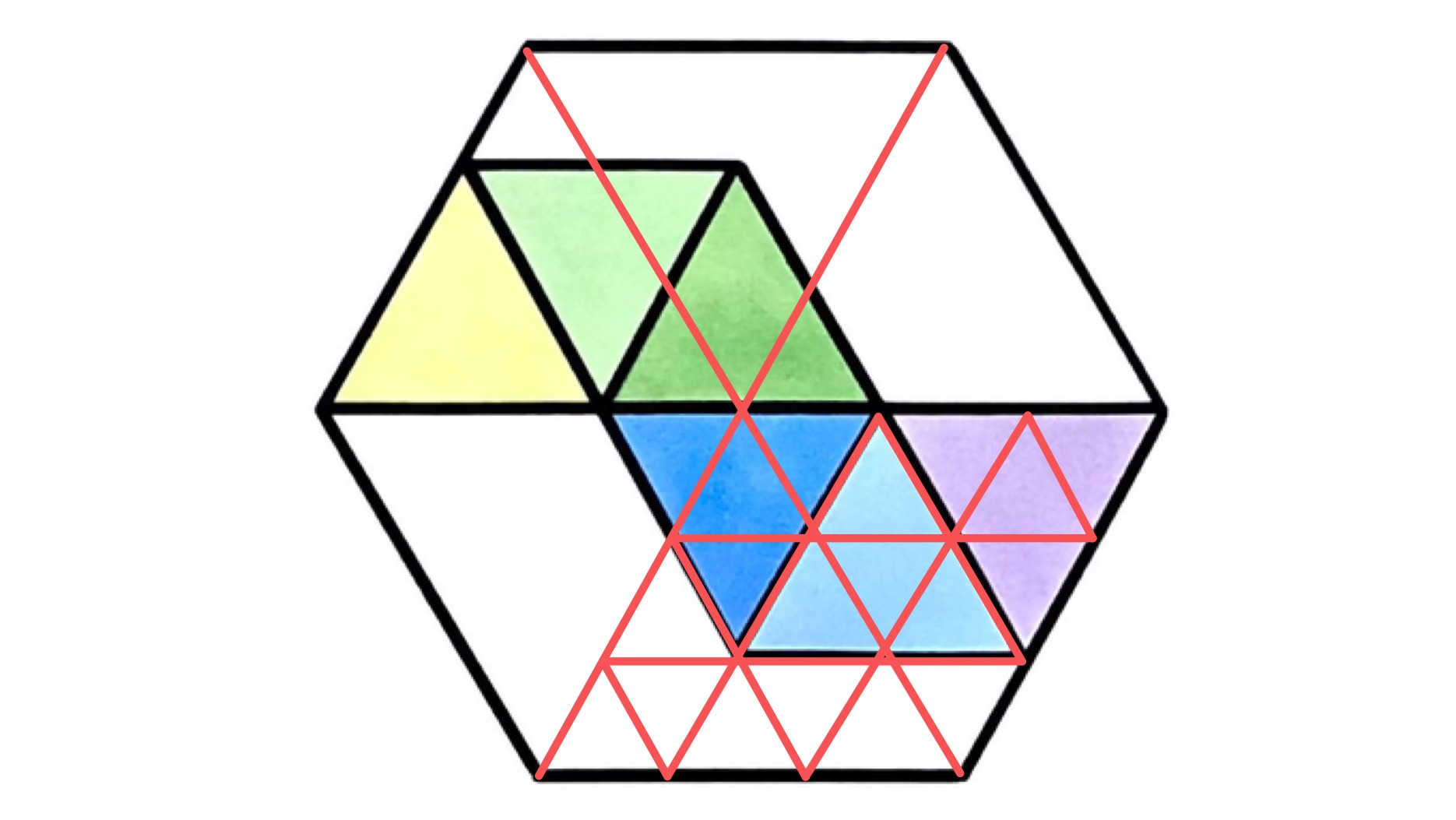
In the above picture, the small triangles have side length one half of that of the original triangles, and so area one quarter of them. Since three of the original triangles stretch across the hexagon, three of the small triangles reaches from a vertex to the centre. Nine of the small triangles therefore form a larger triangle and six of these larger triangles make up the hexagon.
In area, then, we have that the hexagon is six of the larger triangle, which is nine of the smallest triangle, which is a quarter of the original triangle, of which there are six. So in terms of the smallest triangle, the shaded area is and the hexagon is . The shaded area is therefore ths of the hexagon.