Notes
six squares and a quarter circle solution
Solution to the Six Squares and a Quarter Circle Puzzle
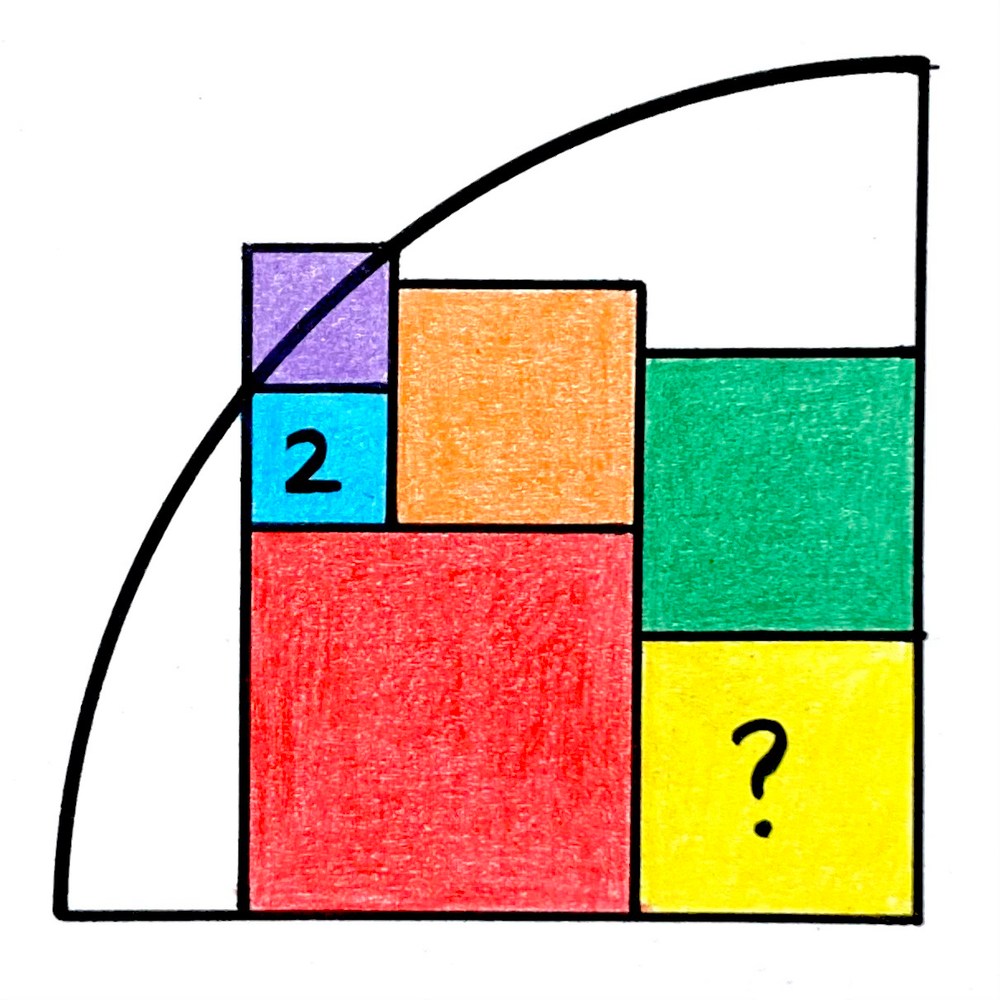
Six squares and a quarter circle. The blue square has area . What’s the yellow area?
Solution by Pythagoras Theorem
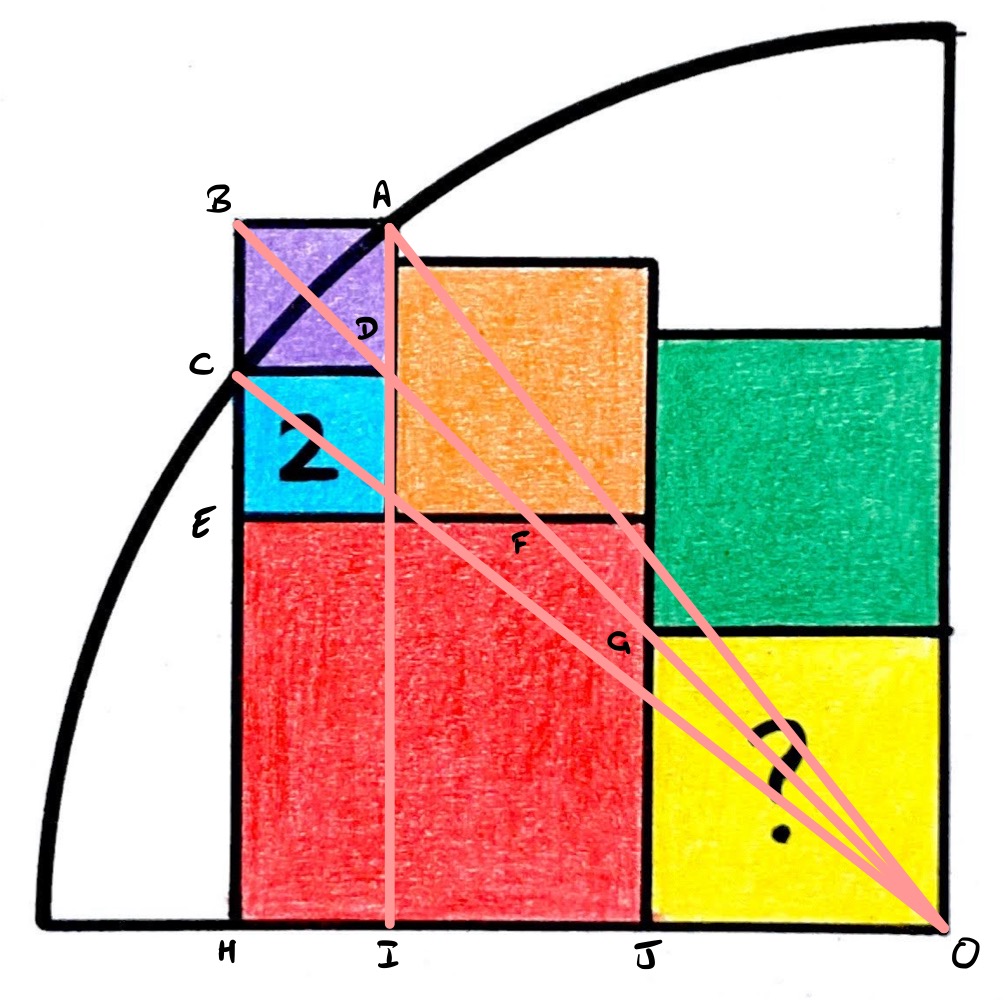
In the diagram above, triangle is a right-angled triangle with hypotenuse a radius of the quarter circle. Triangle is likewise. Therefore, Pythagoras' theorem applies to both.
Let be the radius of the quarter circle, the side length of the yellow square, and the side length of the red square. The side length of the blue square is as it has area . The purple square shares an edge with the blue so also has side length .
Therefore, the sides in triangle are , , and so:
The sides in triangle are , and , so:
Eliminating from this and simplifying proceeds as follows:
Hence the yellow square has area .
Solution by Properties of a Chord and Angles in Parallel Lines
With the points labelled as above, the diagonal of the purple square, is a chord of the quarter circle. Therefore, its perpendicular bisector passes through the centre of the circle at . This perpendicular bisector also aligns with the other diagonal of the square, which is .
Since opposite sides of a square are parallel, line segments and are parallel. Therefore, since corresponding angles in parallel lines are equal, angle is .
This means that triangle is an isosceles right-angled triangle. Hence and have the same length. Removing the side lengths of the red square from both means that has the same length as . That is to say, the yellow square has twice the side length of the blue square and so has four times its area.
The area of the yellow square is therefore .
Solution by Invariance Principle and Properties of a Chord
The size of the red square can be varied, producing several configurations where the relationship between the yellow and blue squares is more straightforward to deduce. All of these still depend on the fact that is a straight line and that varying the size of the red square moves the purple square along that line.
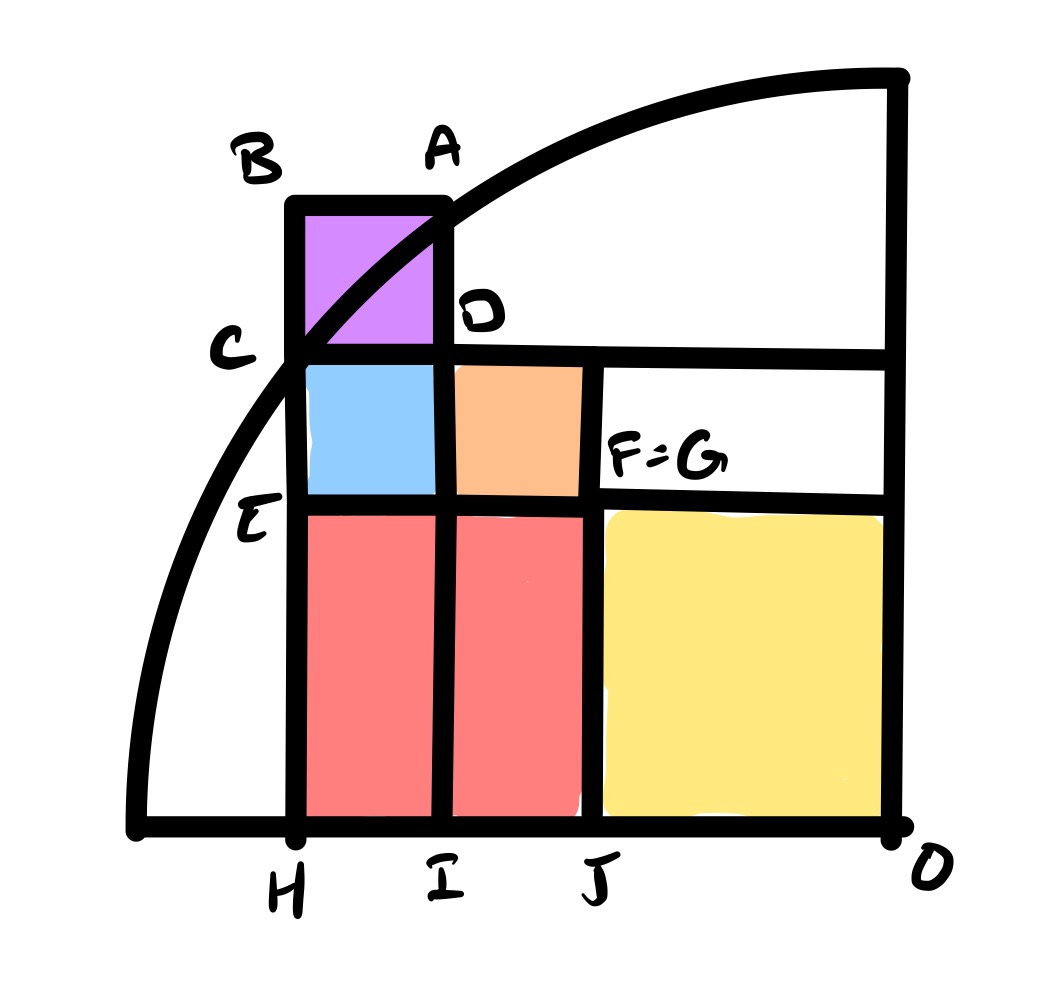
In this configuration, the red square is the same size as the yellow. This brings to , and shows that the orange square is the same size as the blue, whence the red square has twice the side length of the blue. Since the yellow and red are the same size, the conclusion follows.
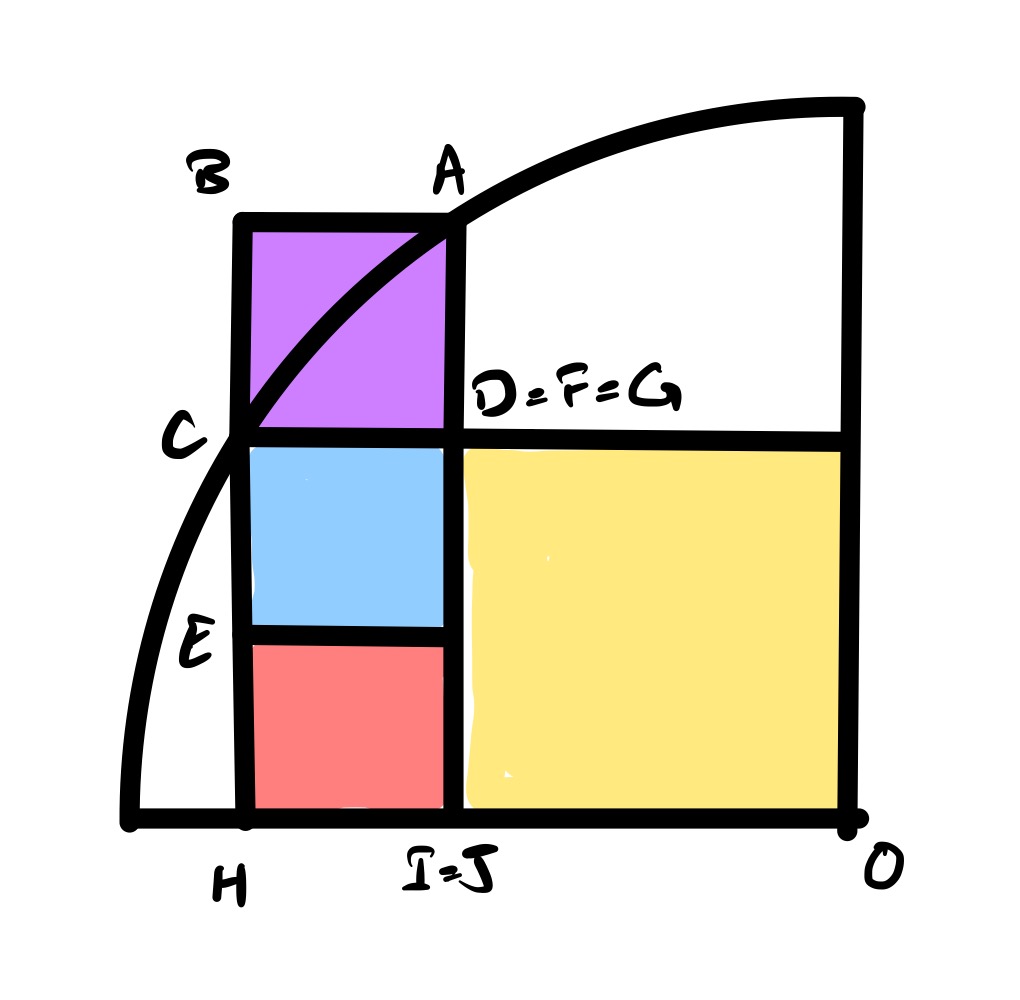
In this configuration, the red square is the same size as the blue. This brings to , and so the yellow square has side length the sum of the side lengths of the blue and red, hence twice that of the blue.
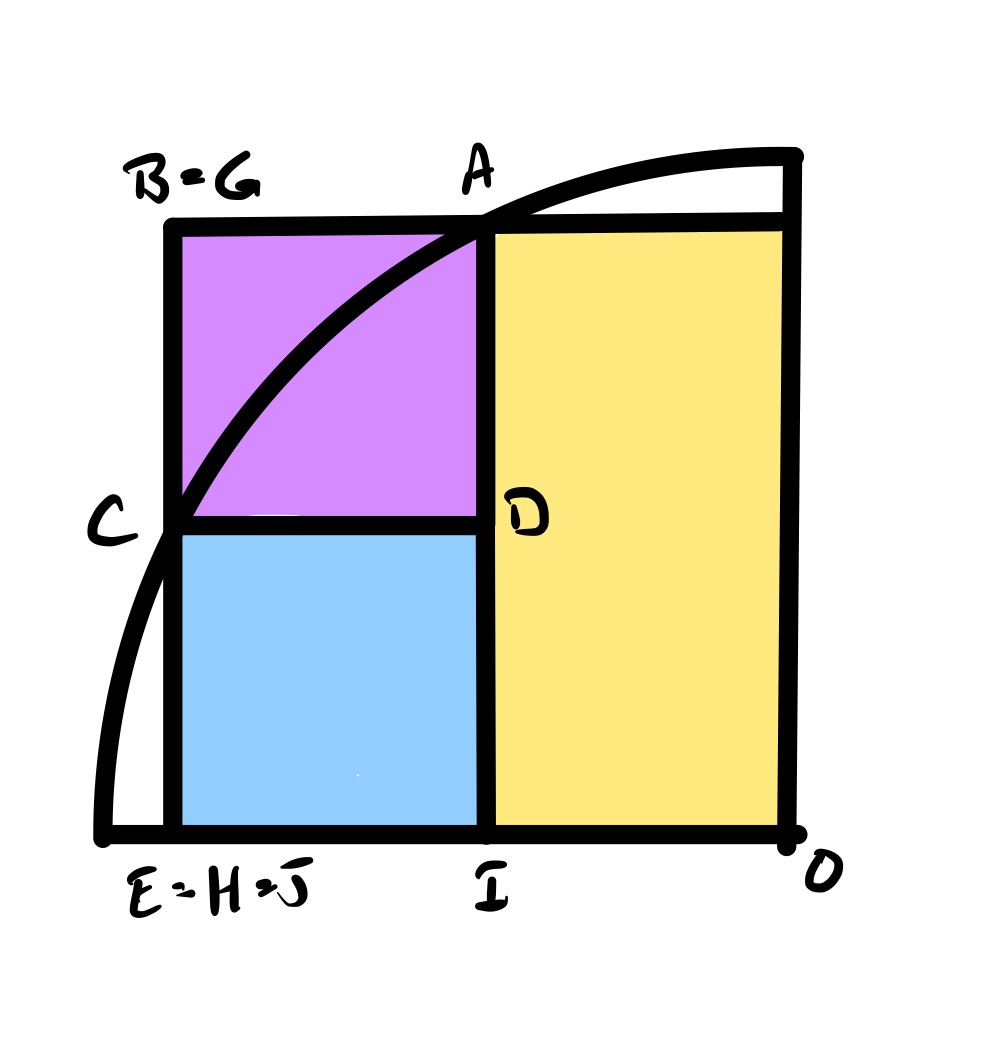
In this configuration, the red square has no size. The blue and purple squares therefore overlap the yellow. The points and overlap, showing that the side length of the yellow is twice that of the blue.
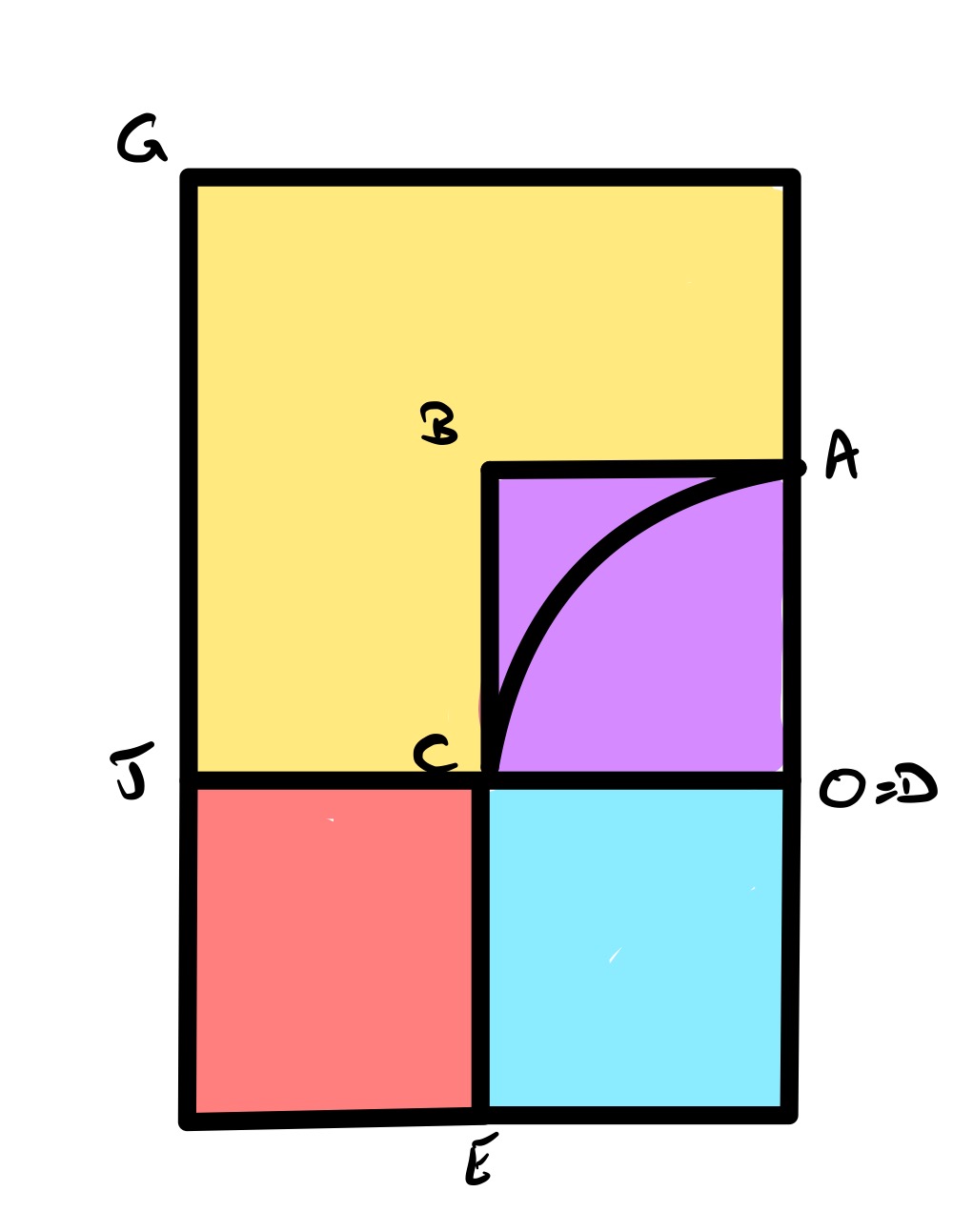
In this configuration, the red square is drawn below the side of the quarter circle. The blue square tracks the red in that its lower left corner is at which is opposite to in the red square. Here, the red square is the same size as the blue and as the purple now lies along , points and must coincide, meaning that the side length of the yellow is the sum of the side lengths of the blue and red.