Notes
six circles inside a circle inside a square solution
Solution to the Six Circles Inside a Circle Inside a Square Puzzle
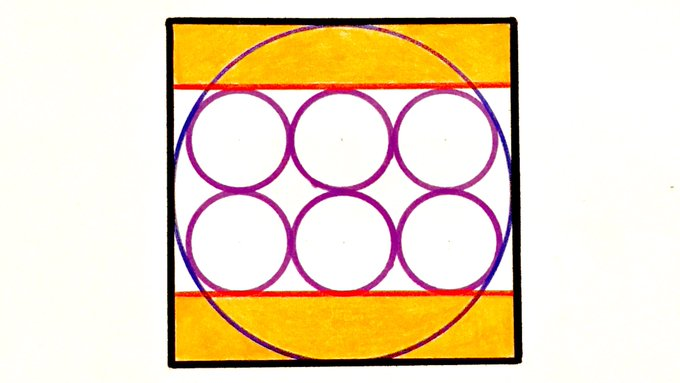
The six small circles each have radius . What’s the total shaded area?
Solution by Pythagoras' Theorem and Lengths in a Circle
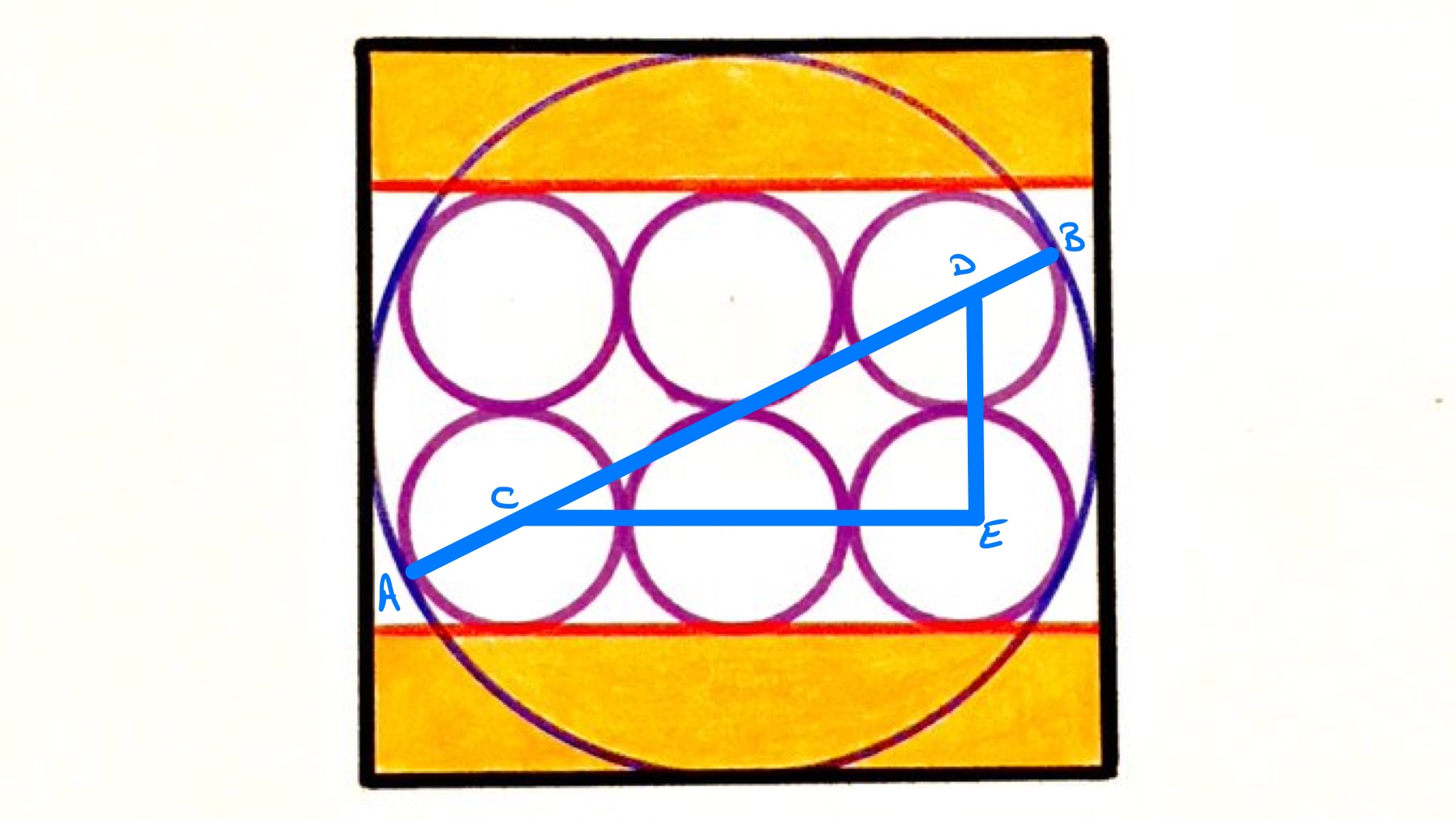
In the above diagram, points and are where the small circles touch the large circle. The line is a diameter of the larger circle and passes through the centres of the lower left and upper right smaller circles, points and respectively. The lengths and are therefore radii of the small circles, and so have length . The point is the centre of the lower right circle and so triangle is right-angled. The length of is then and of is . Applying Pythagoras' theorem to this triangle shows that has length so the length of is .
The width of the square is and the height of the shaded areas is . The shaded area is therefore: