Notes
seven quarter circles inside a semi-circle solution
Solution to the seven quarter circles inside a semi-circle problem
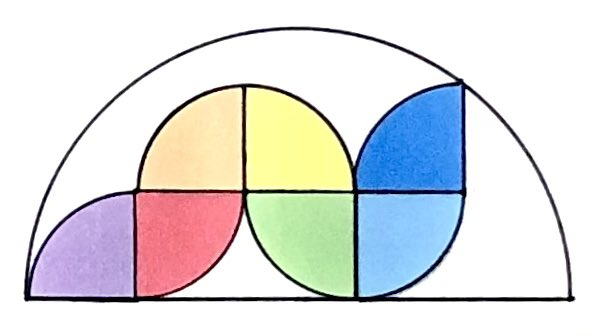
What fraction of the semicircle do these quarter circles cover?
Solution using chords and similar triangles
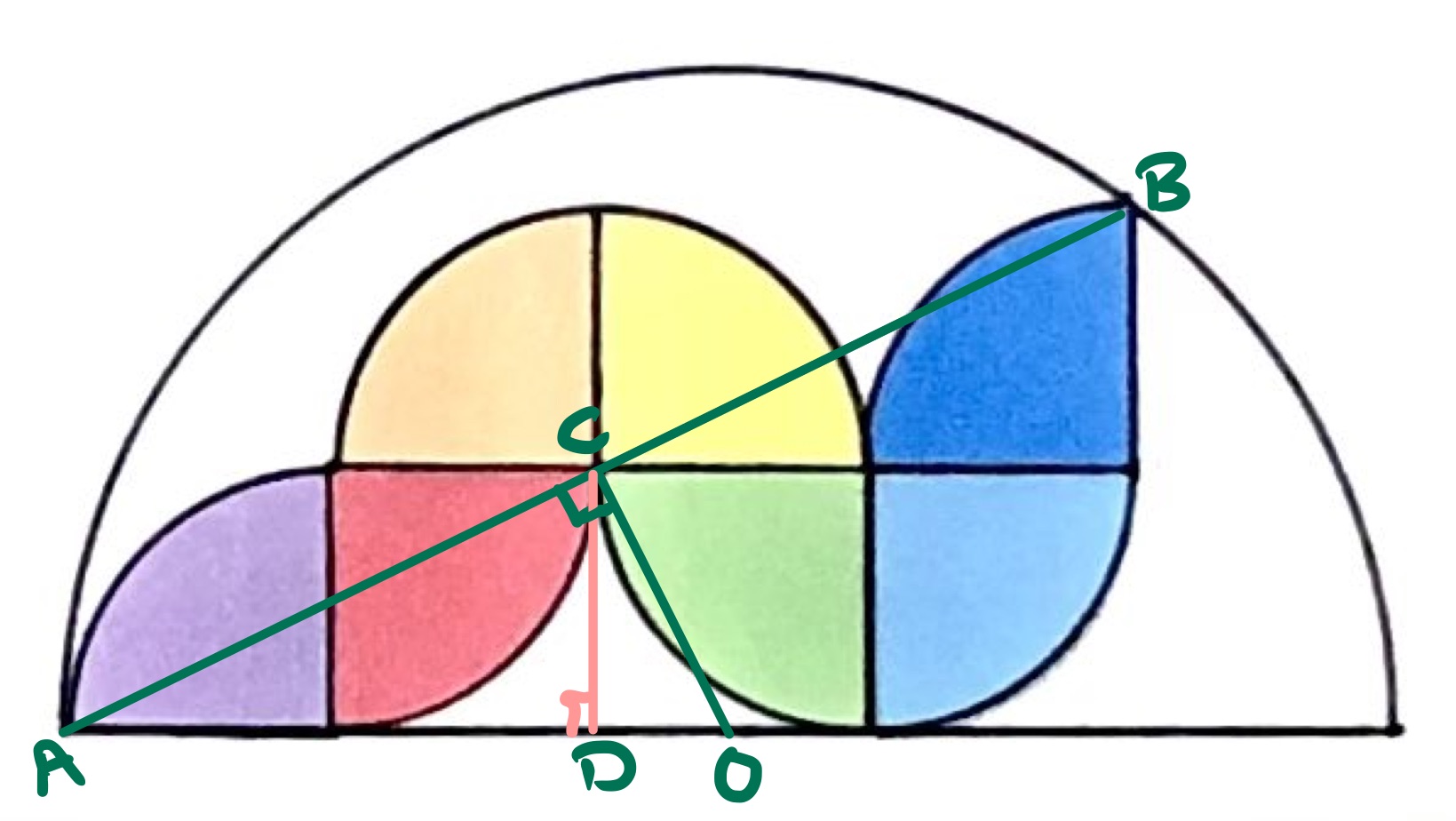
Consider the chord across the diagram. The centre of the circle is located on its perpendicular bisector, which passes through the point . As the base of the semi-circle is a diameter, the centre is therefore at the point where the perpendicular bisector of meets this diameter, marked on the diagram.
Let be the point on the diameter below , so that angle is a right-angle. Then triangles and are similar. As the length is twice that of , so also the length is twice that of . Comparing these to the length of a radius of one of the quarter circles, is therefore times this distance.
The semi-circle is therefore times bigger than one of the quarter circles. There are seven of the quarter circles, so the area of the semi-circle is times bigger than the area of the combined quarter circles. Equivalently, the quarter circles cover an area of the area of the semi-circle.