Notes
seven circles solution

Solution to the Seven Circles Puzzle

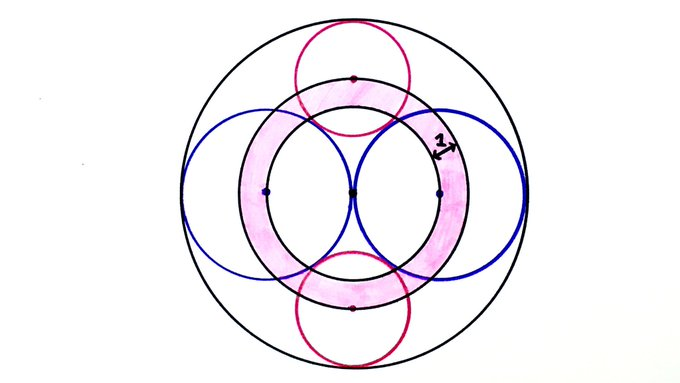
Seven Circles

The centres of all seven circles are marked. The width of the shaded ring is $1$ . What’s its area?

Solution by Pythagoras' Theorem

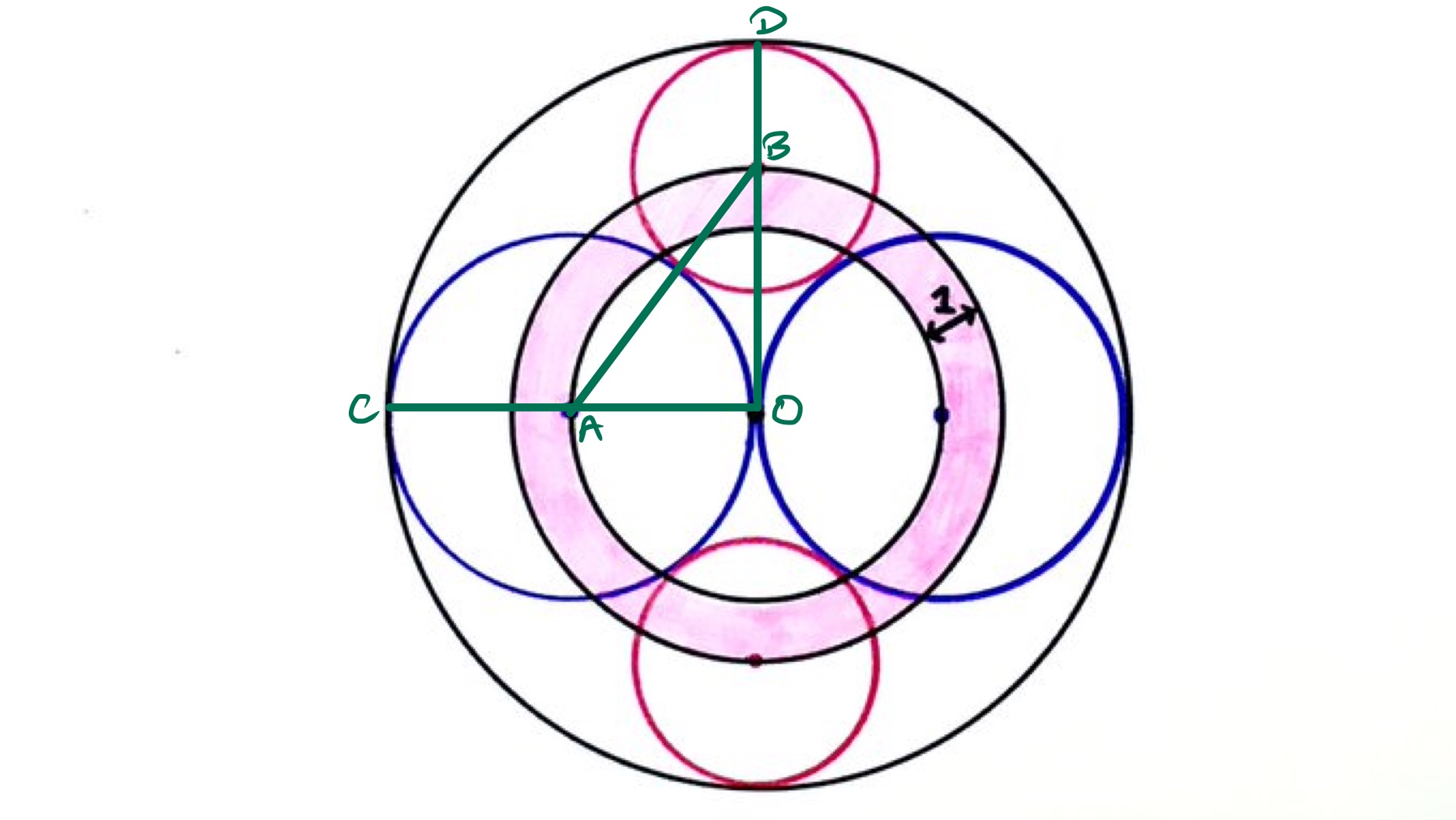
Seven circles labelled

Let $a$ be the radius of the blue circles (and therefore also of the inner black circle) and let $b$ be the radius of the pink. Then $O C$ has length $2 a$ and $O D$ has length $a + 1 + b$ . As these are radii of the outer circle, they are equal and so $a = b + 1$ . The length of $A B$ is $a + b = 2a - 1$ so by applying Pythagoras' theorem to triangle $O A B$ , the following equation for $a$ is obtained:

\begin{aligned} a^2 + (a + 1)^2 &= (2 a - 1)^2 \\ 2 a^2 + 2 a + 1 &= 4 a^2 - 4 a + 1 \\ 2 a^2 - 6 a &= 0 \\ a &= 3 \end{aligned}

The area of the pink ring is then:

\pi (a + 1)^2 - \pi a^2 = (2 a + 1) \pi = 7 \pi

Created on August 19, 2021 19:13:09 by Andrew Stacey

Notes seven circles solution

Solution to the Seven Circles Puzzle

Solution by Pythagoras' Theorem

Notes
seven circles solution