Notes
semi-circles in a rectangle solution
Solution to the Semi-Circles in a Rectangle Puzzle
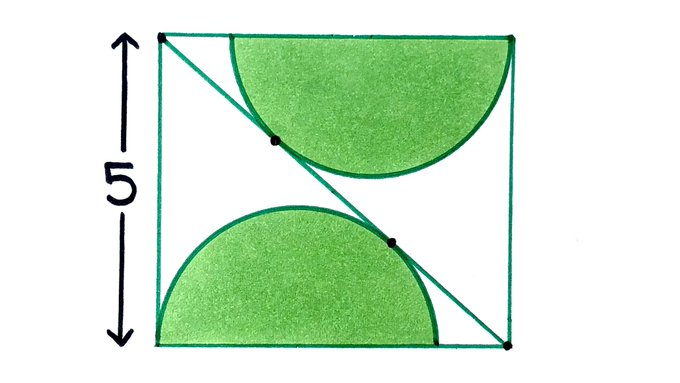
The dots are equally spaced along the rectangle’s diagonal. What’s the total shaded area?
Solution by Angle Between a Radius and Tangent, Similar Triangles, and Pythagoras' Theorem
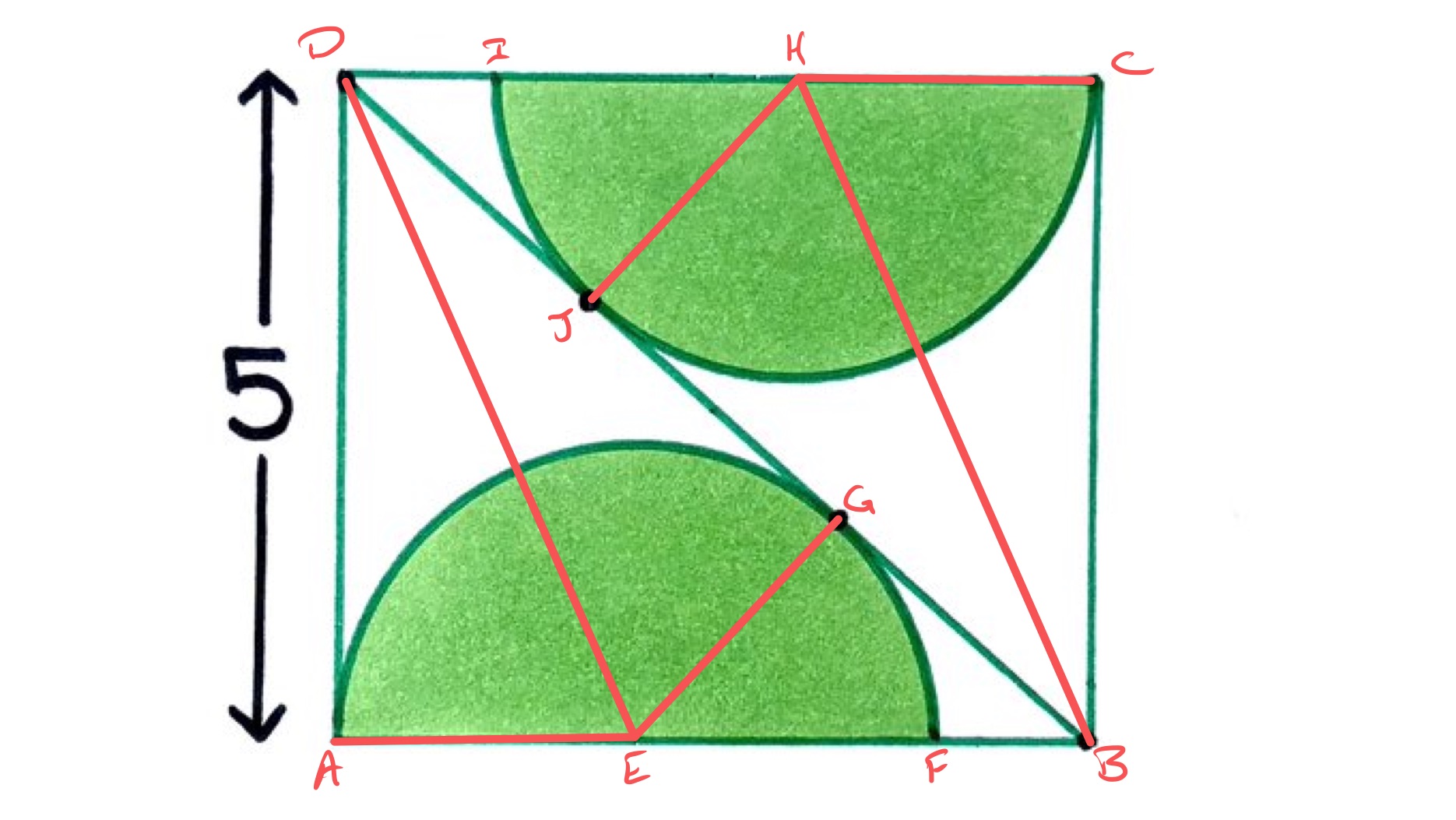
With the points labelled as above, and are the centres of their respective semi-circles.
Since is tangent to the semi-circle centred at , angle is the angle between a radius and tangent and so is . Triangle is therefore a right-angled triangle. Triangle is also right-angled. The line segment is the hypotenuse of both, and the sides and are radii of the same circle so have the same length. Triangles and are therefore congruent which means that the line segments and have equal length. Since and are evenly spaced along , has length . Applying Pythagoras' theorem to triangle then shows that the length of is:
Triangle is also right-angled. It shares angle with triangle and so these triangles are similar with corresponding to . Therefore the lengths of and are in the ratio , meaning that the points and divide in the ratio and so the radius of the semi-circle is of the length of , namely .
The area of the two semi-circles is therefore .