Notes
semi-circle splitting a triangle solution
Semi-Circle Splitting a Triangle
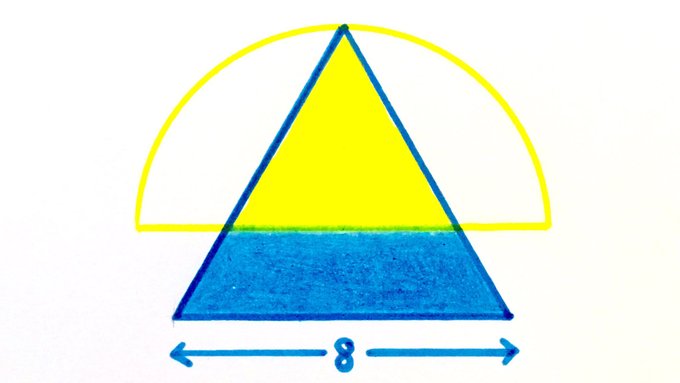
The equilateral triangle has been split into two equal areas. What’s the area of the semicircle?
Solution by Area Scale Factor and Lengths in Equilateral Triangles
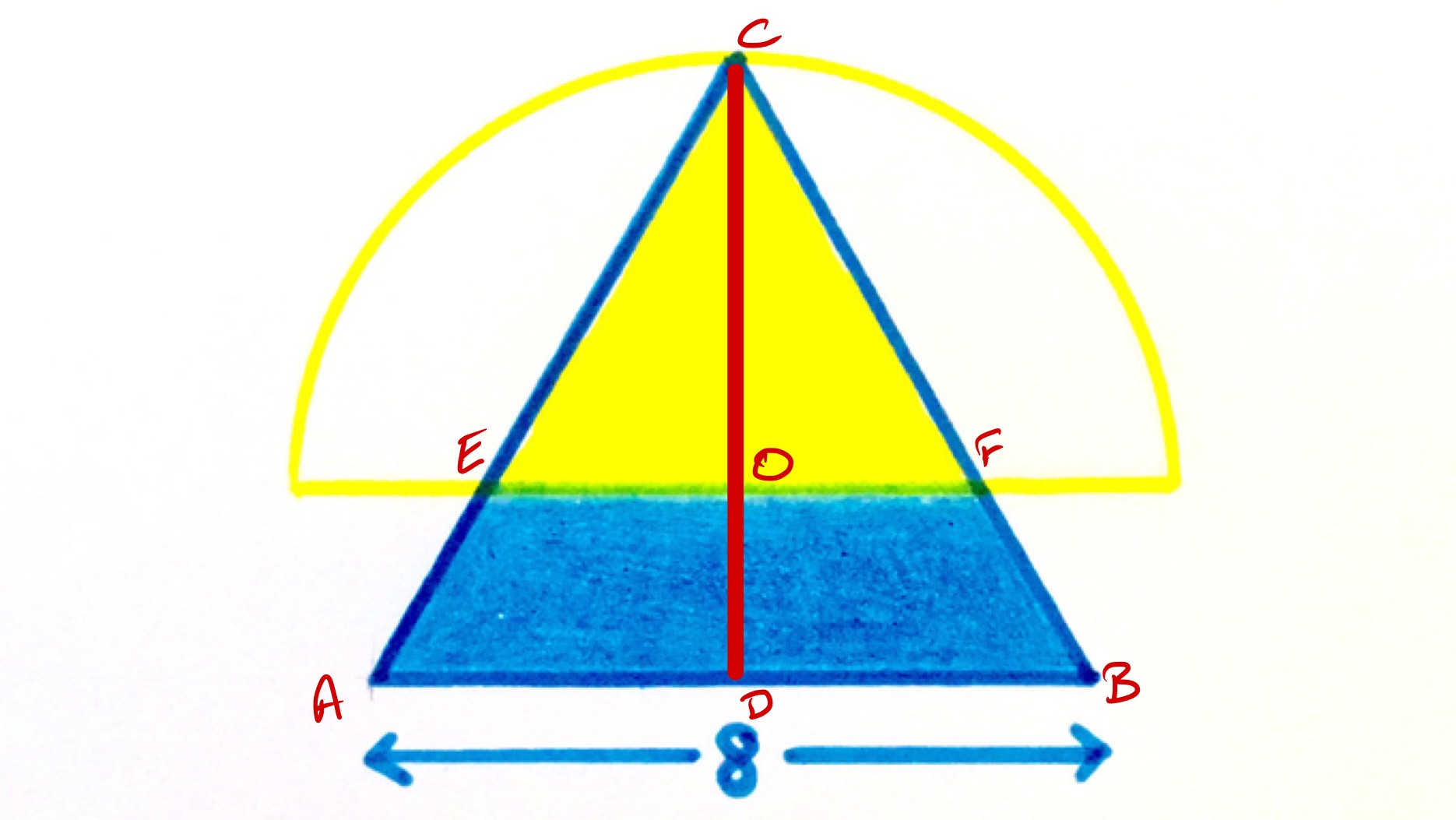
With the points labelled as above, the orange triangle has half the area of the full triangle, so the length of is of the length of , so is . The height is then times the length of , so is . The area of the semi-circle is therefore .