Notes
semi-circle in a square solution
Solution to the Semi-Circle in a Square Puzzle
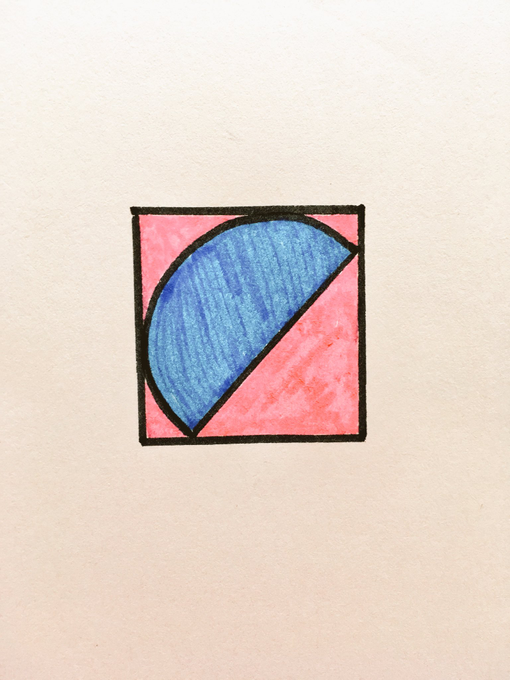
Is more of this square pink or blue? How would you prove it?
Solution by Angle Between a Radius and Tangent, Isosceles Right-Angled Triangles, Area of a Circle, and Area of a Square
SemiCircleinaSquareLabelled.png
In the above diagram, the point labelled is the centre of the semi-circle. The point labelled is where the semi-circle touches the top edge of the square, so as the angle between a radius and tangent is , is perpendicular to . Similarly, is perpendicular to .
The line segments and are radii of the circle, so are of the same length. Therefore, and are of the same length. Triangles and are congruent since is parallel to and so angles and are corresponding angles, and and have the same length. So and have the same length so triangle is isosceles.
Let be the radius of the semi-circle. Then as is an isosceles right-angled triangle with hypotenuse of length , its shorter sides both have length . The side length of the square is therefore . Its area is thus
The area of the semi-circle is .
To compare these two, consider the decimal representations of the circle area and half the area of the square, since if the blue area is larger than the pink then it will be over half the square and vice-versa:
Therefore the blue area is larger.