Notes
semi-circle in a square in a quarter circle solution
Solution to the Semi-Circle in a Square in a Quarter Circle Puzzle
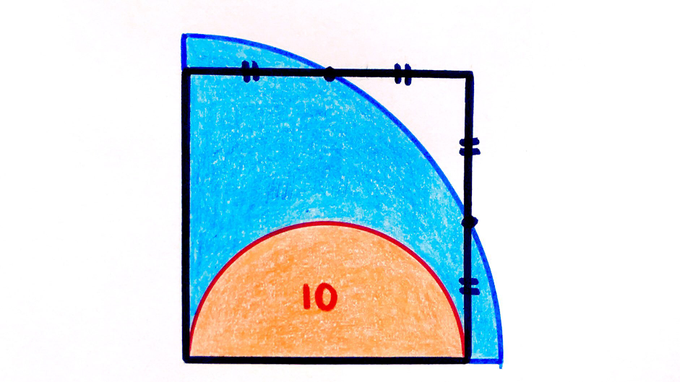
The orange area is . What’s the blue area?
Solution by Pythagoras' Theorem
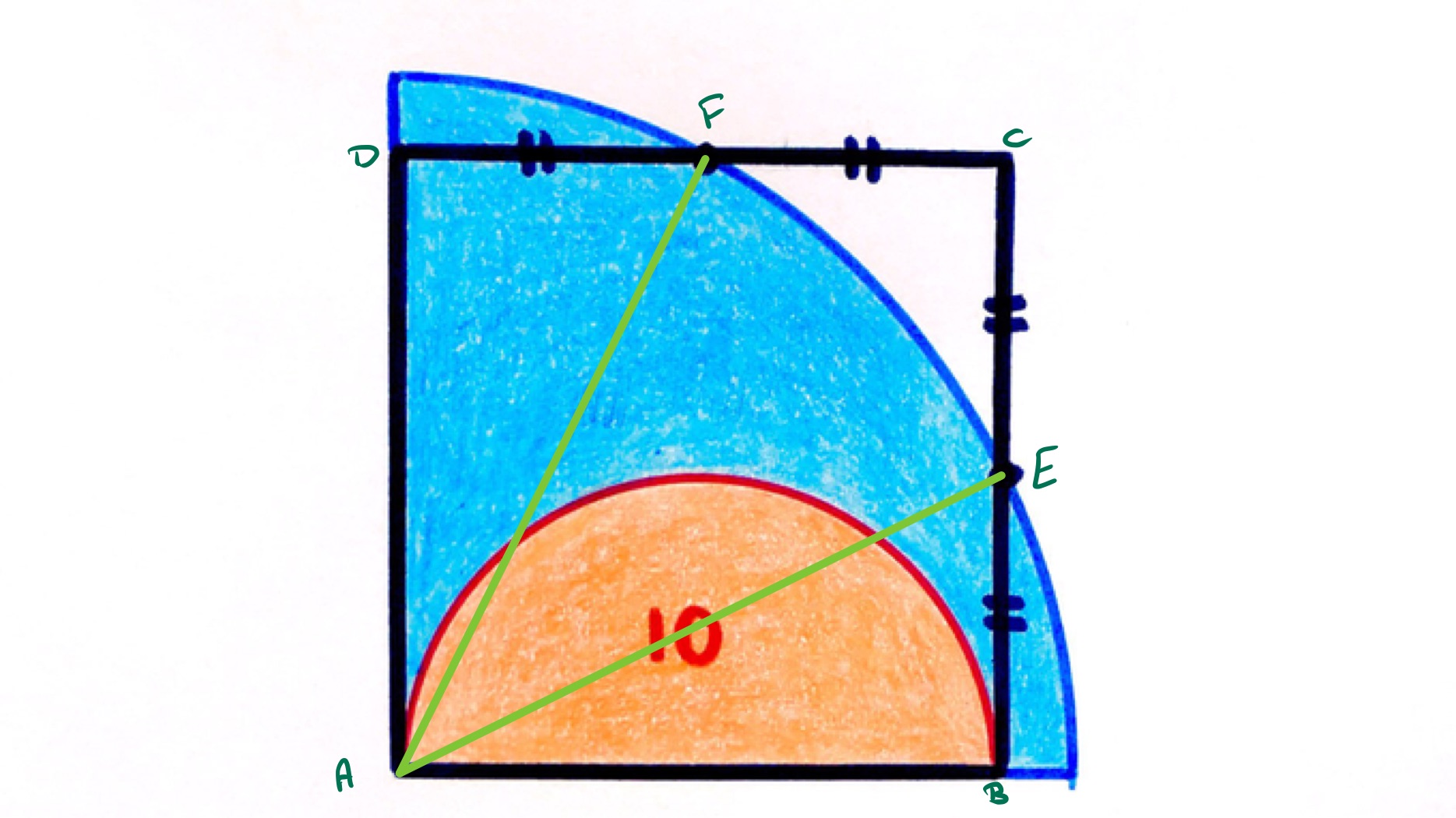
The quadrilateral is not given as a square, but can be shown to be one. Firstly, and are tangent to the circle at the ends of the diameter , so as the angle between a radius and tangent is a right-angle, the edges and are perpendicular to . The quadrilateral has edges and of equal length as each other, as are and , so is a kite. The line through and is therefore a line of symmetry, and since is a continuation of and of by the same lengths, reflection in the line is also a line of symmetry of . Therefore has the same length as , and angle is also a right-angle. This is enough to establish as a square.
This also shows that the total shaded region is a quarter circle.
Let be the radius of the orange semi-circle and the radius of the outer quarter circle. Then the quarter circle has area and the semi-circle has area , this latter being equal to . The length of an edge of the square is then .
As is the midpoint of , the length of is half of the length of the side of the square, so is . Applying Pythagoras' theorem to the triangle shows that:
The area of the quarter circle is therefore . The blue area is then .