Notes
semi-circle in a right-angled triangle solution
Solution to the Semi-Circle in a Right-Angled Triangle Puzzle
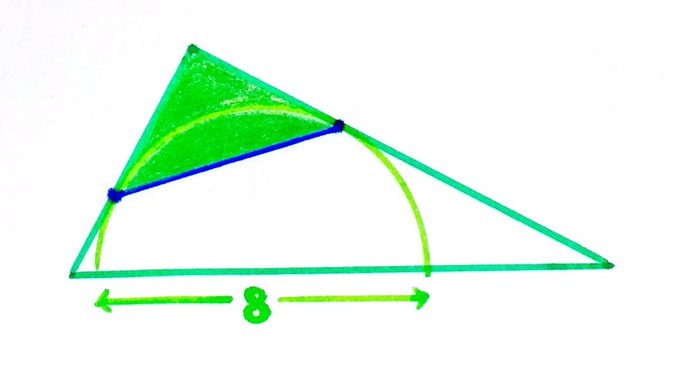
A semi-circle sits in a right-angled triangle. What’s the shaded area?
Solution by Angle Between a Radius and Tangent
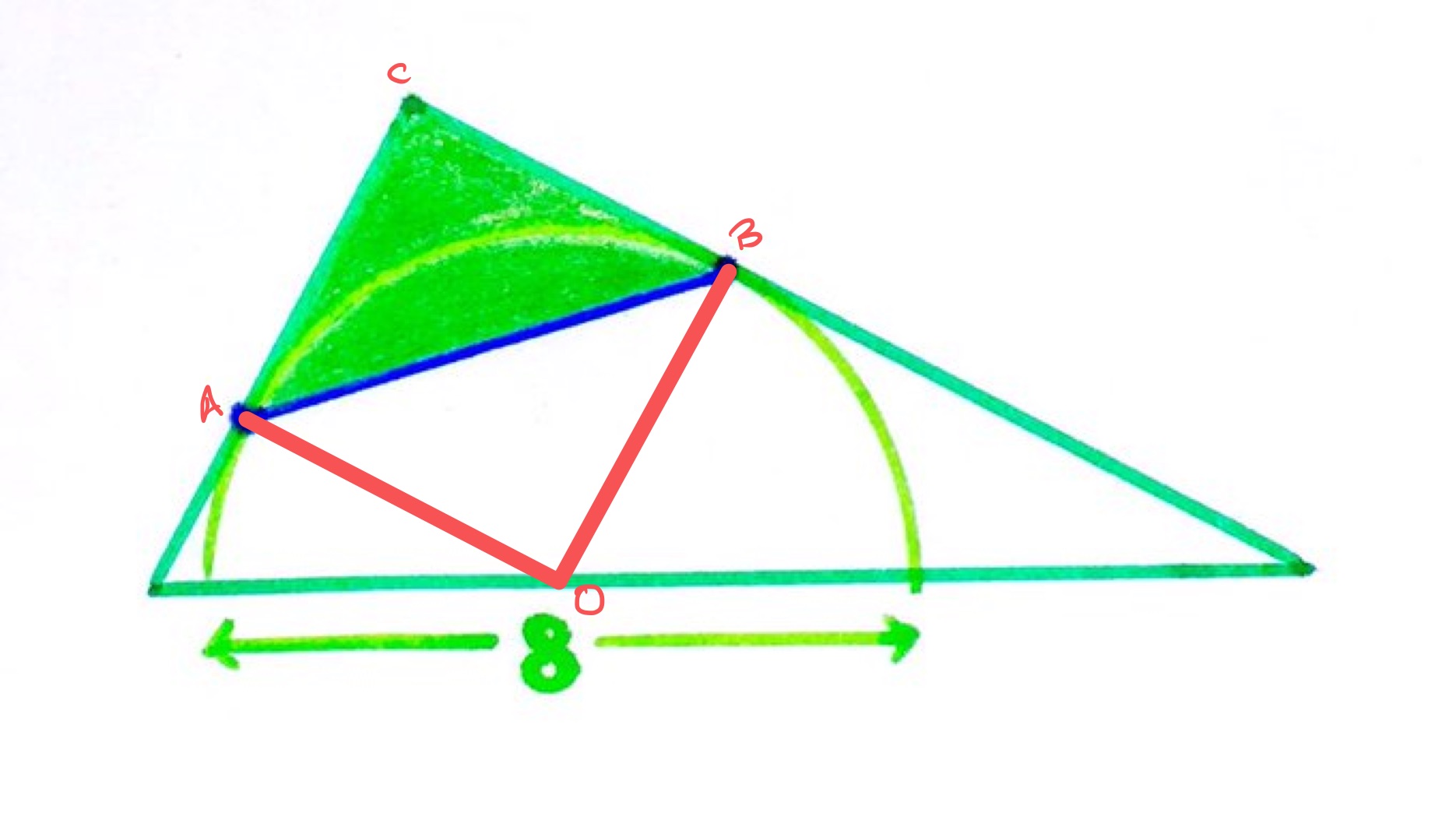
With the points labelled as in the diagram above, the point labelled is the centre of the circle.
Angles and are both right-angles as they are the angle between a radius and tangent. Angle is given as a right-angle. Therefore, quadrilateral is a rectangle. The lengths of and are equal as they are radii of the semi-circle, so in fact is a square. As the diameter of the semi-circle is , the side length of the square is and its area is . The triangle is half of that square and so has area .