Notes
semi-circle in a circle solution
Solution to the Semi-Circle in a Circle Puzzle
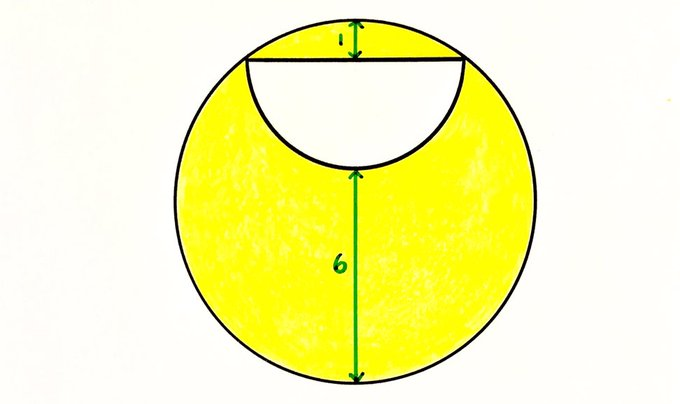
What fraction of the circle is shaded?
Solution by Intersecting Chords Theorem
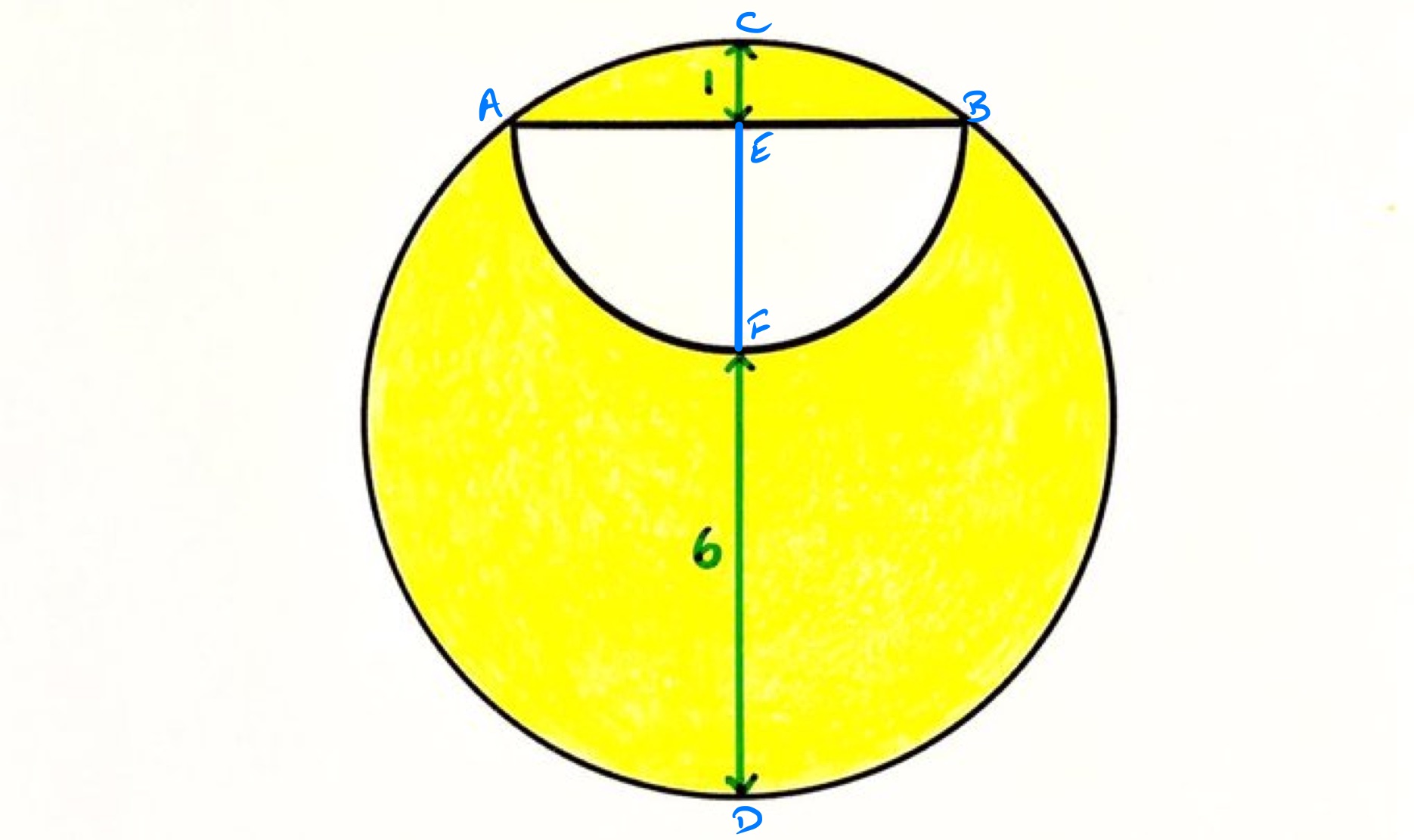
In the diagram above, let be the radius of the inner semi-circle. So is the length of each of , , and . The length of is then so applying the intersecting chords theorem to and results in:
This has solution (the other possible solution is but as is a length this isn’t possible).
The diameter of the outer circle is so its area is . The area of the inner semi-circle is . Therefore ths of the circle is shaded.