Notes
semi-circle between two quarter circles solution
Solution to the Semi-Circle Between Two Quarter Circles Puzzle
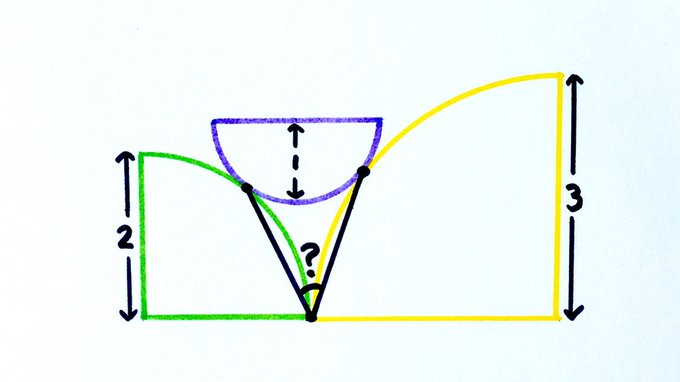
What’s the angle?
Solution by Pythagoras' Theorem, Isosceles Triangle, Angles in a Triangle, and Angles at a Point on a Straight Line
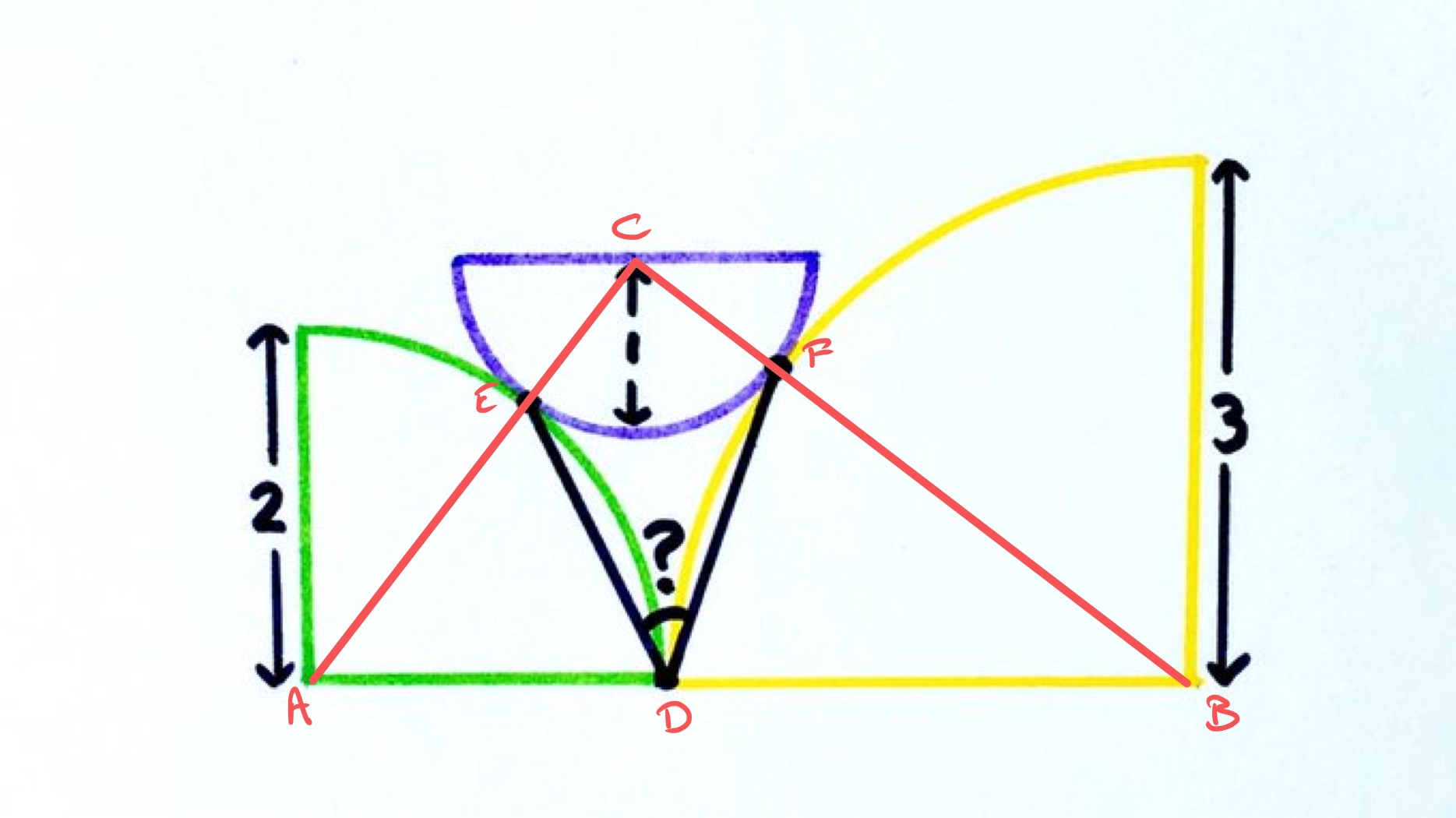
Joining the centres passes through the points where the part circles meet. The lengths of each then are the sums of the radii, so are , , and . Since , this means that triangle is right-angled by Pythagoras' theorem with the right-angle at . So angles and sum to . Let be angle and angle , so .
As triangle is isosceles and the angles in a triangle sum to , angle is . Similarly, angle is . Since angles at a point on a straight line add up to , angle is therefore given by: