Notes
semi-circle and tangents in a square solution

Semi-Circle and Tangents in a Square

Solution by Angle Between a Radius and Tangent and Similarity

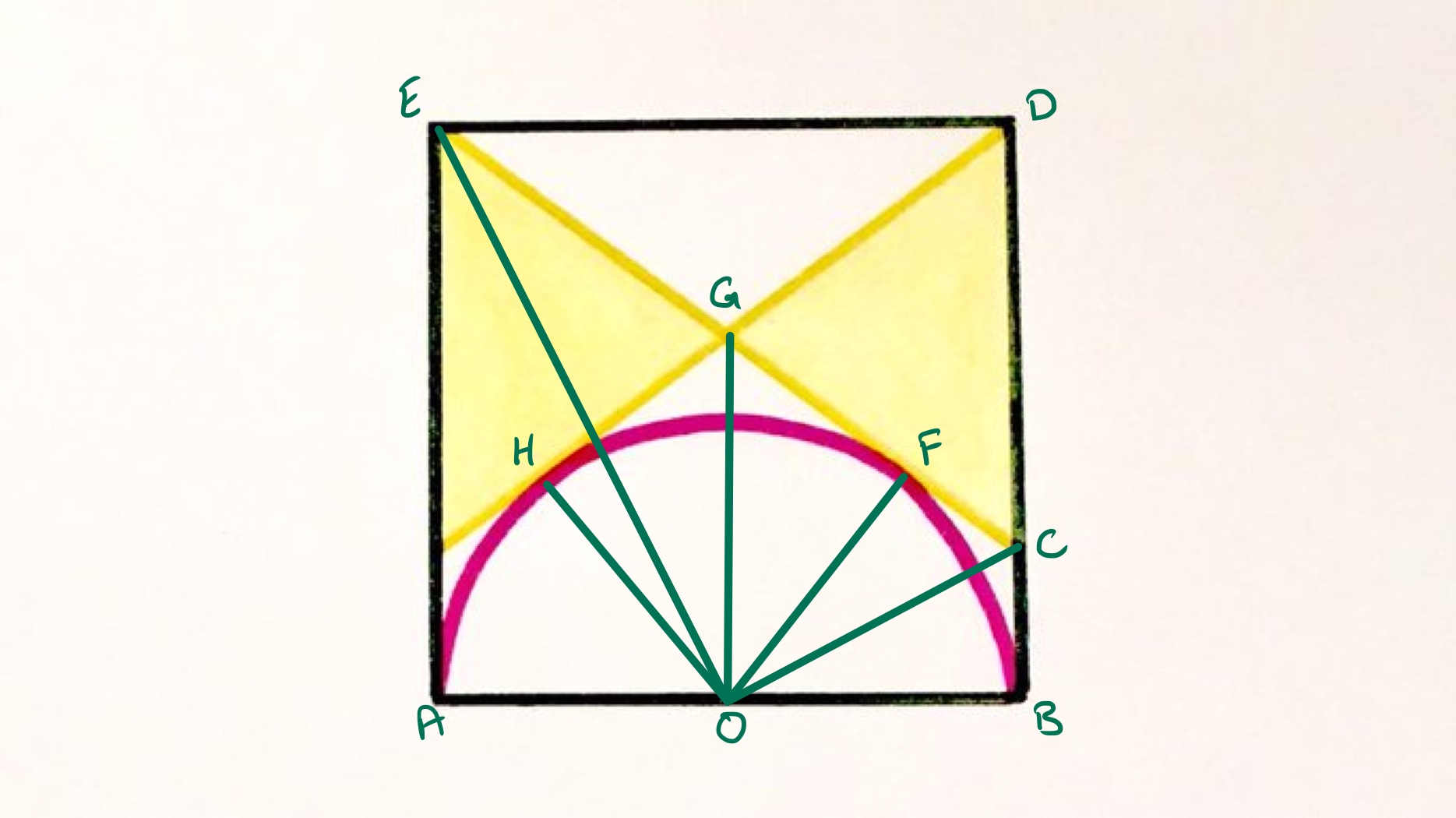
Since the angle between a radius and tangent is $90^\circ$ and the angles in a quadrilateral add up to $360^\circ$, angles $F \hat{C} B$ and $B \hat{O} F$ add up to $180^\circ$, therefore angle $F \hat{C} B$ is the same as angle $F \hat{O} A$. This shows that the kites $B C F O$ and $A O F E$ are similar. Since $A E$ is the same length as the diameter of the semi-circle, the scale factor is $2$. Therefore the length of $C B$ of half of that of $O B$, and so a quarter of the length of the side of the square. Setting $x$ to be the side length of the square, the area of the shaded region is then $2 \times \frac{1}{2} \times \frac{1}{2} x \times \frac{3}{4} x = \frac{3}{8} x^2$ and so $\frac{3}{8}$ths of the square is shaded.

Solution by Pythagoras' Theorem

The lengths of $C B$ and $C F$ are the same as $B C F O$ is a kite, similarly $F E$ and $A E$ have the same length. With $x$ the length of the side of a square and $y$ the length of $C B$, applying Pythagoras' theorem to triangle $E C D$ gives:

This simplifies to $4 x y = x^2$ and so $x = 4 y$. This shows that $C B$ is a quarter of the length of the square. The calculation of the area continues from there as above.