Notes
region of an octagon solution

Region of an Octagon

Solution by Isosceles Right-angled Triangles

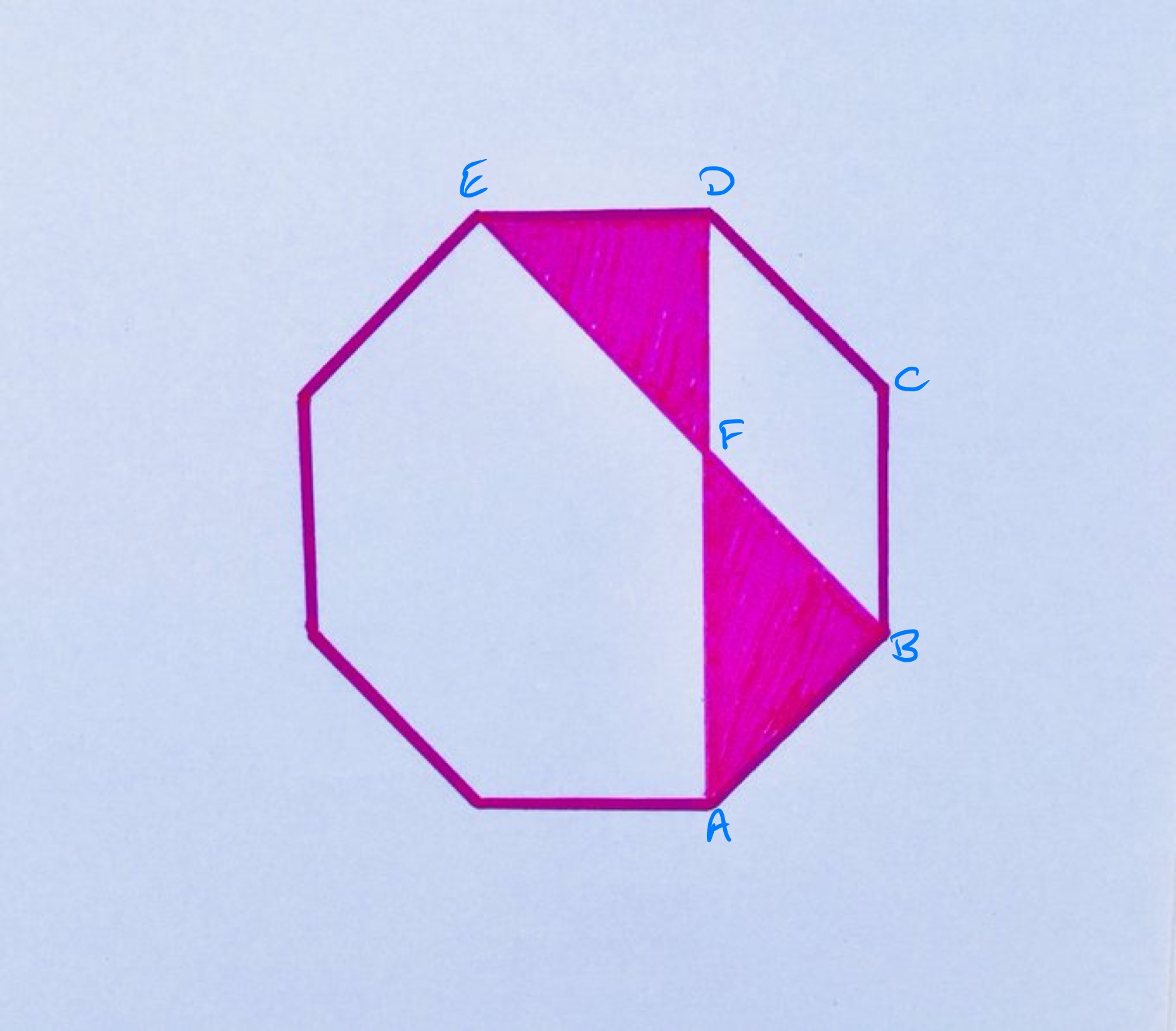
With the points labelled as above, $D A$ is perpendicular to $E D$, and $E B$ is at $45^\circ$ to $E D$, so triangle $E D F$ is an isosceles right-angled triangle. Let $E D$ have length $a$, then triangle $E D F$ has area $\frac{1}{2} a^2$. The same applies to triangle $A B F$, so the shaded region has area $a^2$. The perimeter of the octagon is $8 a$, so $8 a = a^2$ and hence $a = 8$, so the common value for the area of the shaded region and the perimeter of the octagon is $64$.