Notes
rectangles stacked in a semi-circle solution
Rectangles Stacked in a Semi-Circle
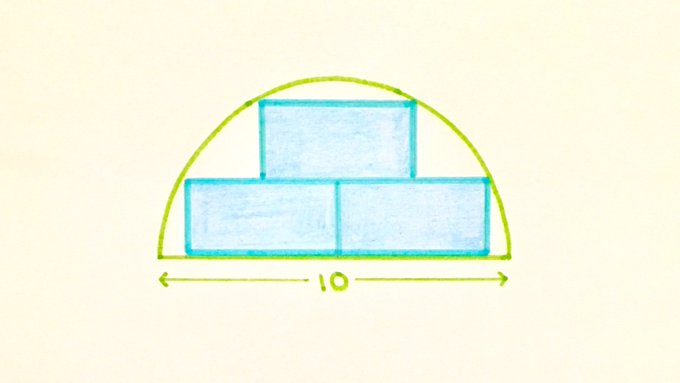
Three identical rectangles are stacked inside a semicircle. Find the total shaded area.
Solution by Pythagoras' Theorem
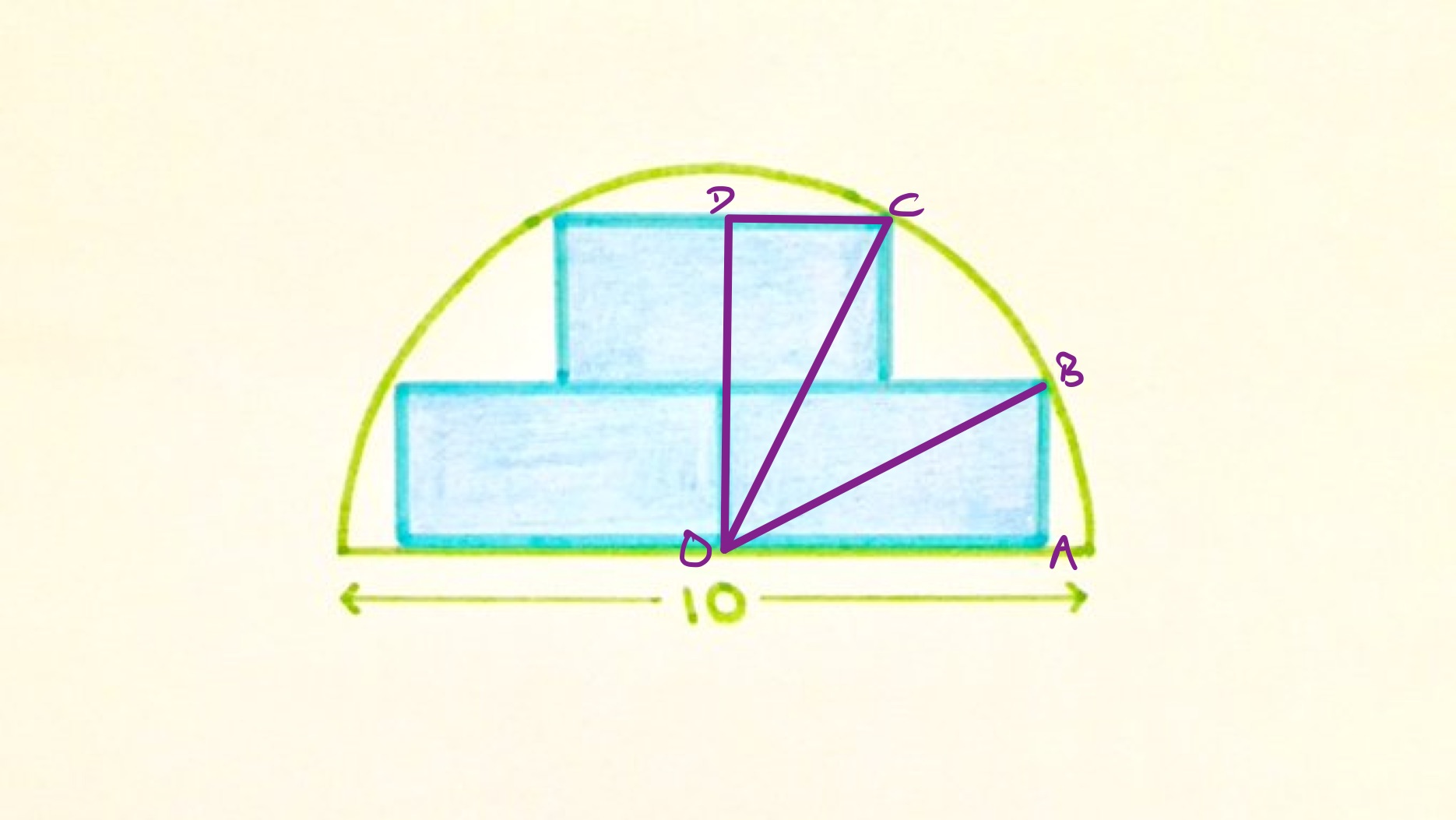
With the points labelled as above, let be the length of and the length of . As the rectangles are identical, has length . The radius of the circle is , so has length . Applying Pythagoras' theorem to triangle shows that:
Then also has length and has length , so applying Pythagoras' theorem to triangle shows that:
Subtracting these equations shows that . Since both and are lengths, and so positive, this means that , and . The area of a single rectangle is , so the area of all three is .