Notes
rectangle quartered by semi-circles solution
Solution to the Rectangle Quartered by Semi-Circles Puzzle
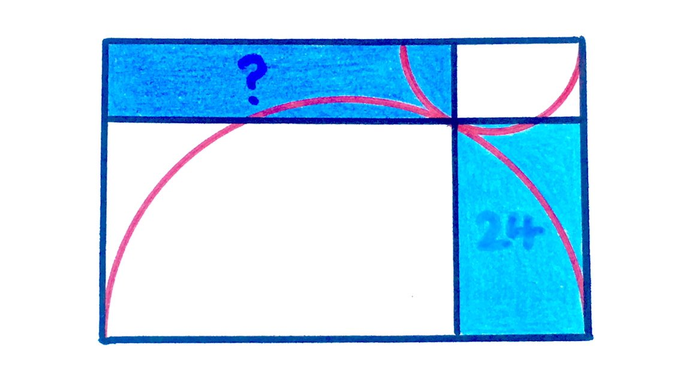
What’s the area of the dark blue rectangle?
Solution by Alternate Angles and Similar Triangles
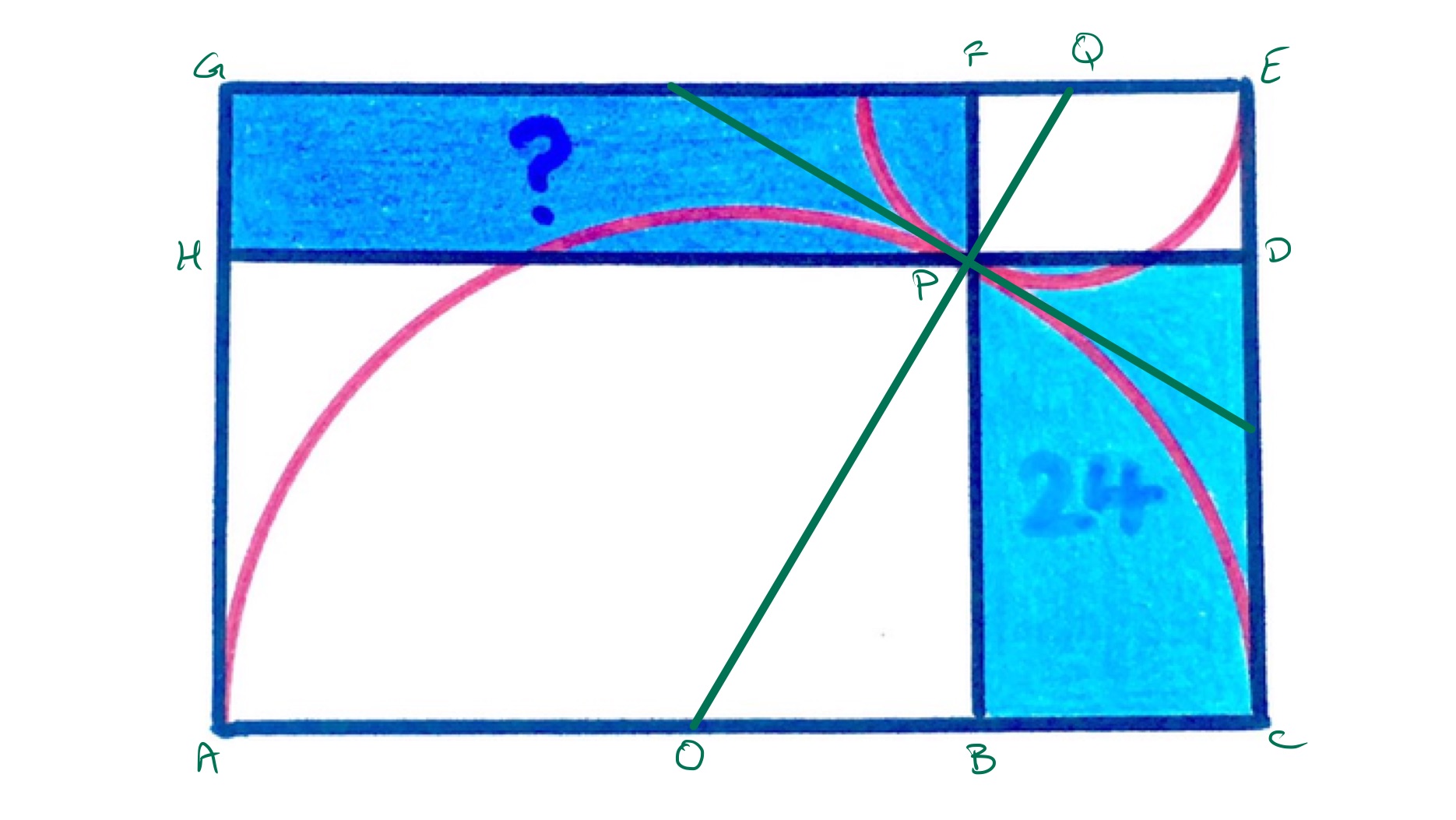
In the above diagram, the points labelled and are the centres of their respective semi-circles. The line passes through the point where the circles touch. Angles and are alternate angles so are equal and thus triangles and are similar triangles. Since and are radii of the semi-circle, they have the same length; similarly, and have the same length. Therefore, the lengths of and are in the same ratio as those of and . Replacing by and by in that leads to:
which rearranges to and so the blue rectangles have the same area, which is .