Notes
rectangle overlapping a circle solution
Solution to the Rectangle Overlapping a Circle Puzzle
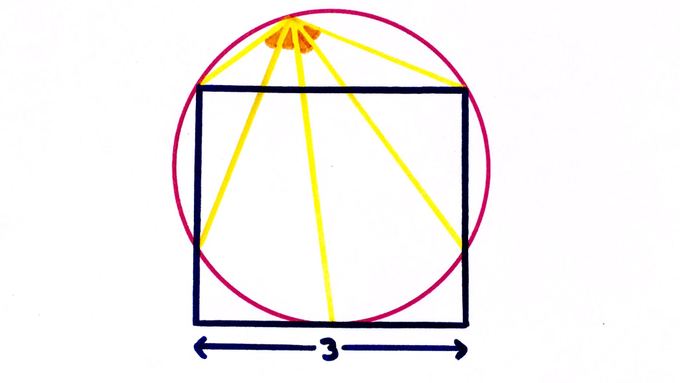
The four marked angles are equal. If the rectangle’s width is , what’s the area of the circle?
Solution by Angle in a Semi-Circle and Angles in the Same Segment
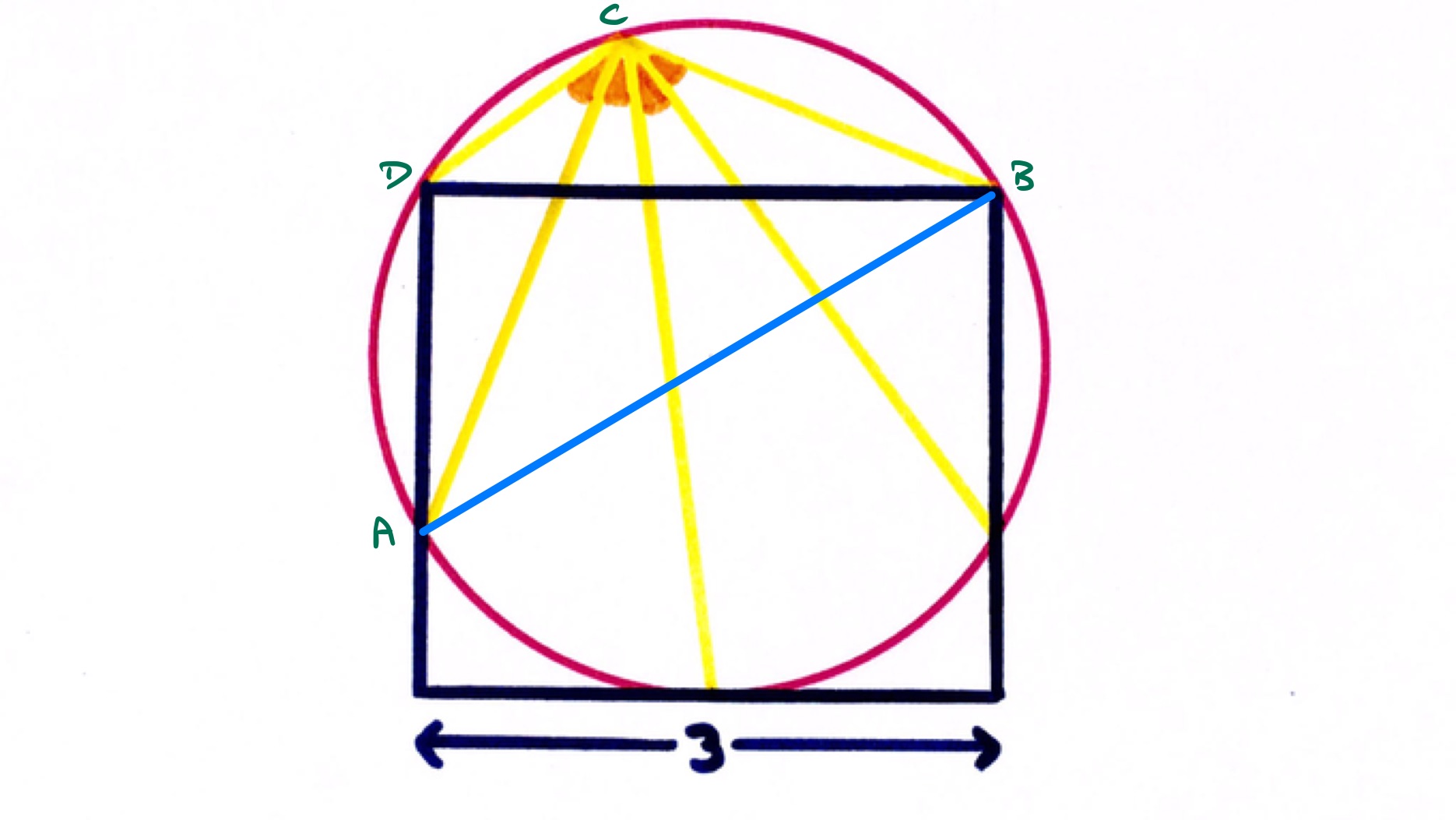
With the points labelled as in the diagram, angle is a right-angle so using the result that the angle in a semi-circle is a right-angle, is a diameter of the circle. Then by the same result, angle is also a right-angle. This means that the marked angle is .
Angle is then and so as angles in the same segment are equal, angle is also . So triangle is a right-angled triangle, which means it is half an equilateral triangle. This means that the length of is times the length of , so has length and the radius of the circle is therefore . Its area is then .