Notes
rectangle across a rectangle solution
Solution to the Rectangle Across a Rectangle Puzzle
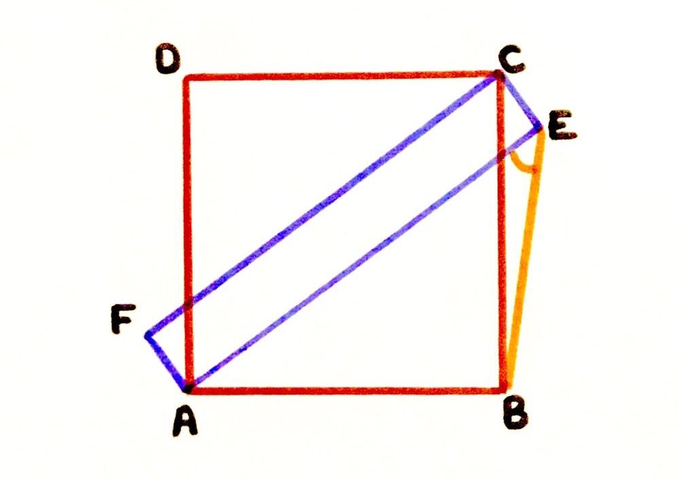
Here are two rectangles. , , . What’s the angle?
Solution by Angle at the Circumference is Half the Angle at the Centre
Let be the length of the diagonal . Applying Pythagoras' theorem to the right-angled triangle shows that satisfies . Now let be the length of , so the height of rectangle . Applying Pythagoras' theorem to shows that , so and . As this is the same length as , the rectangle is actually a square.
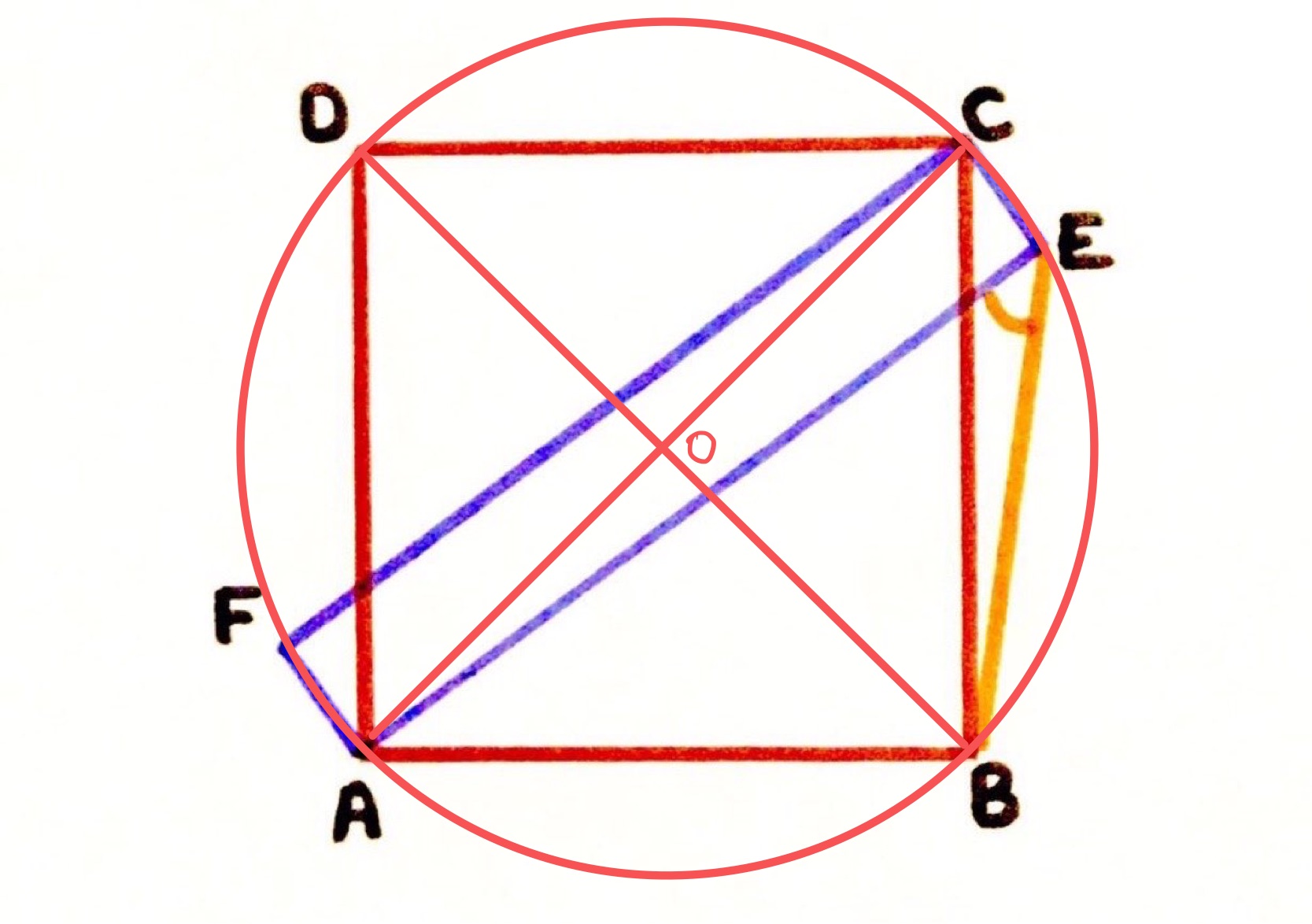
Now, as in the above diagram, consider the circumcircle of the square , with the point labelled at its centre. This also passes through the vertices of the other rectangle as the points and are on it. Since the angle at the circumference is half the angle at the centre, angle is half of angle . This latter angle is , hence .