Notes
rectangle, circle, and triangle solution
Solution to the Rectangle, Circle, and Triangle Puzzle
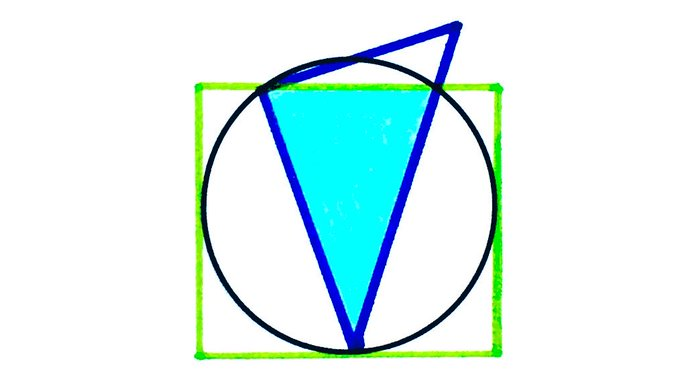
A rectangle, a circle, and a triangle. What fraction of the rectangle is shaded?
Solution by Properties of Chords, the Intersecting Chords Theorem, and Similar Triangles
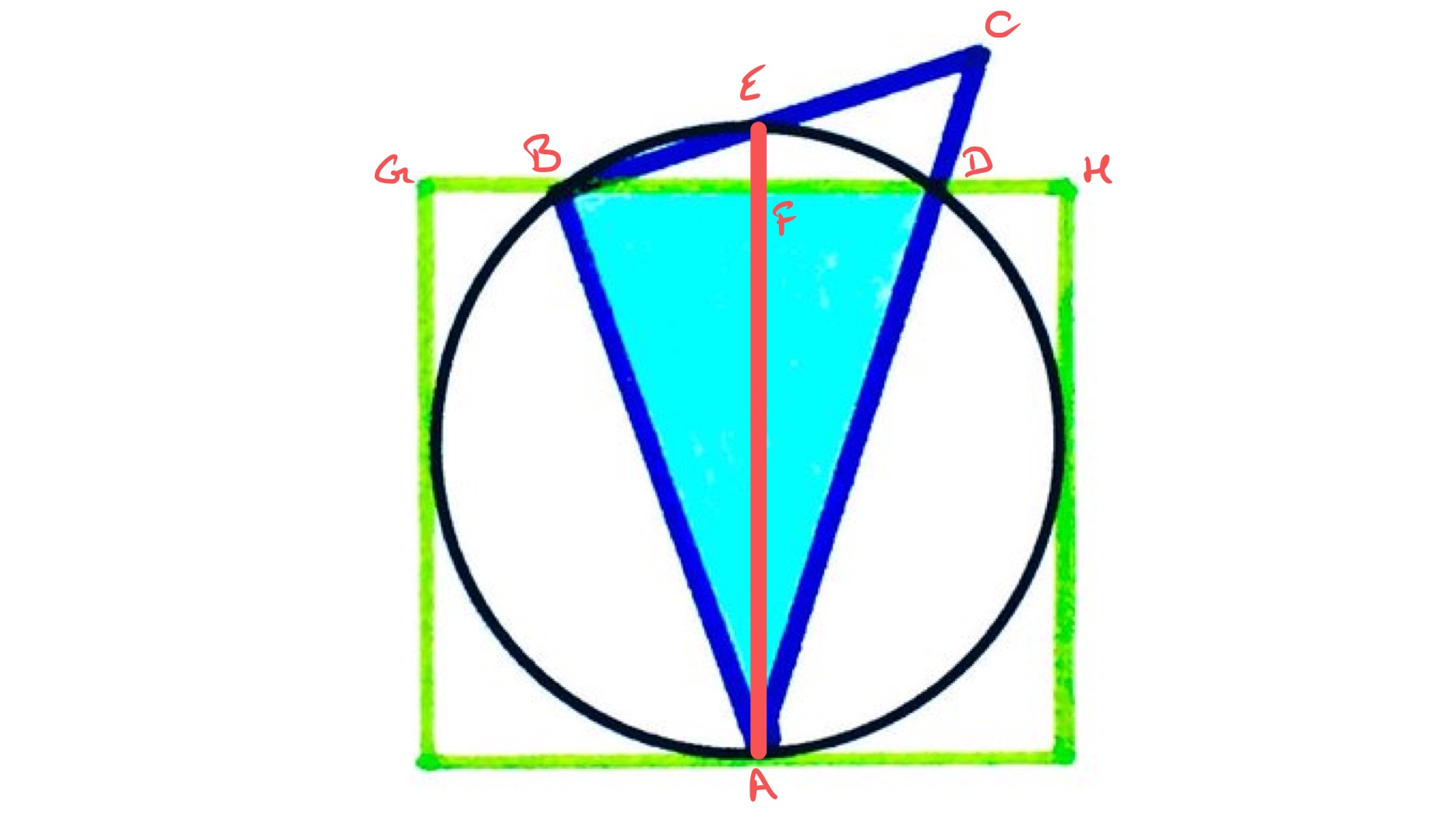
With the points labelled as above, triangle has a right-angle at so since the angle in a semi-circle is , is a diameter of the circle. Then as is a chord of the circle and is perpendicular to this chord and passes through the centre of the circle, it must pass through the midpoint of . Therefore has the same length as , which is .
Applying the intersecting chords theorem to the chords and shows that:
So the length of is meaning that the length of is . Therefore is times the length of .
Triangles and are both similar to triangle , so the length of is times that of , and of is times of . Putting these together, is of the length of .
As the rectangle and triangle have the same “height”, the fraction of the rectangle that is shaded is given by comparing half the length of to the length of . Half the length of is the length of , and the length of is a diameter of the circle, which has the same length as . Therefore ths of the rectangle is shaded.