Notes
quarter circles in a square in a circle solution
Solution to the Quarter Circles in a Square in a Circle Puzzle
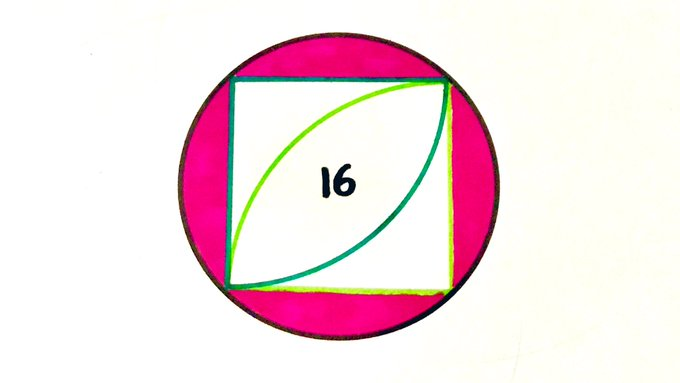
The area where these two quarter circles overlap is . What’s the total shaded area?
Solution by Area Scale Factor
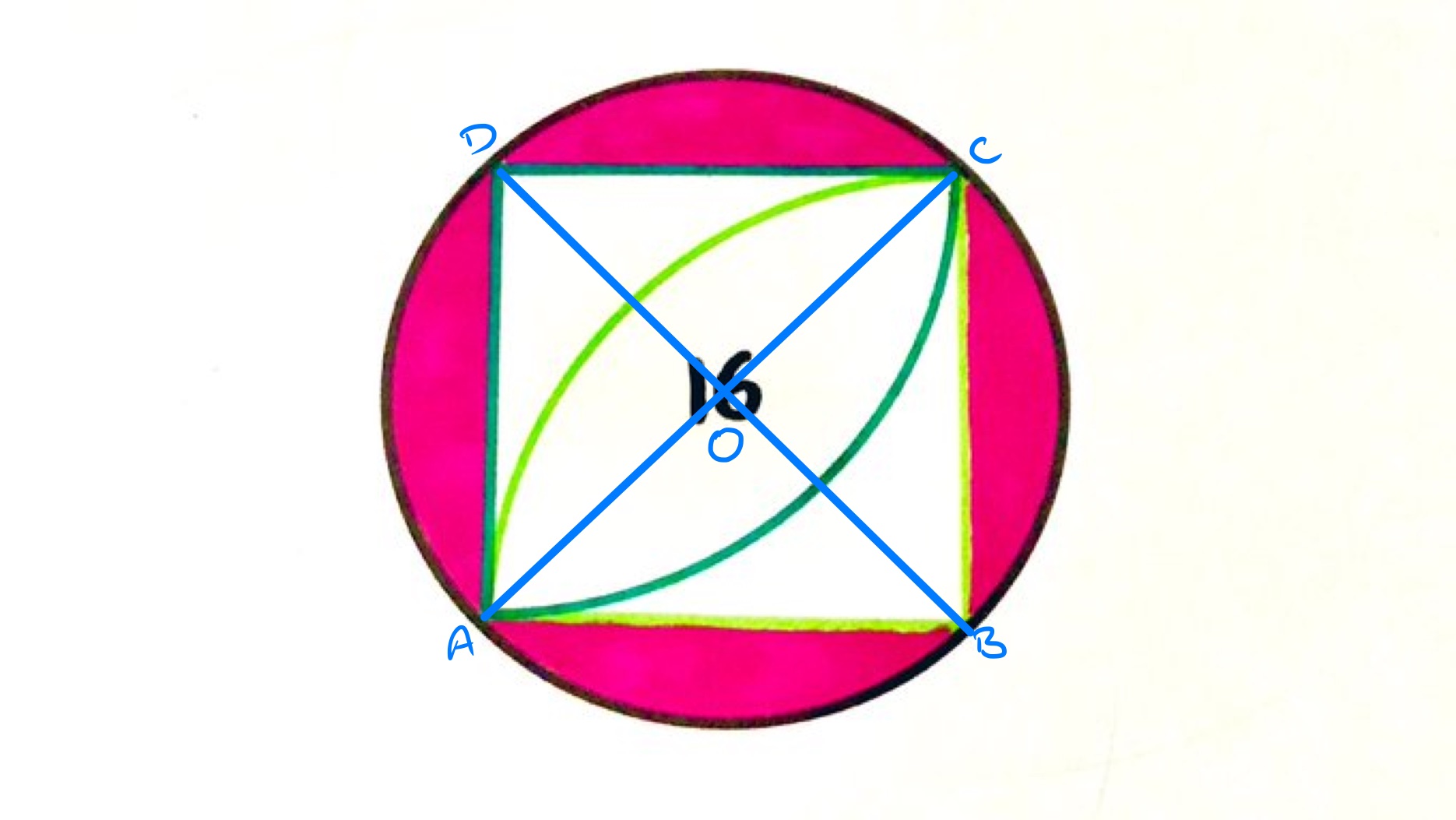
The radius of the quarter circles is the length of the side of the square and the radius of the outer circle is half the diameter of the square. Therefore, the radius of the outer circle is times the radius of the quarter circle.
The overlap of the quarter circles can be cut in two along the line , then each piece has area . Each of those pieces is the curved region of a quarter circle, so is similar to each of the four pieces that make up the shaded region. The length scale factor is so the area scale factor is . Each of the four shaded regions therefore has area , so the total shaded area is .