Notes
quarter circles in a rectangle solution

Quarter Circles in a Rectangle

Solution by Equilateral Triangles and Angle Between a Radius and Tangent

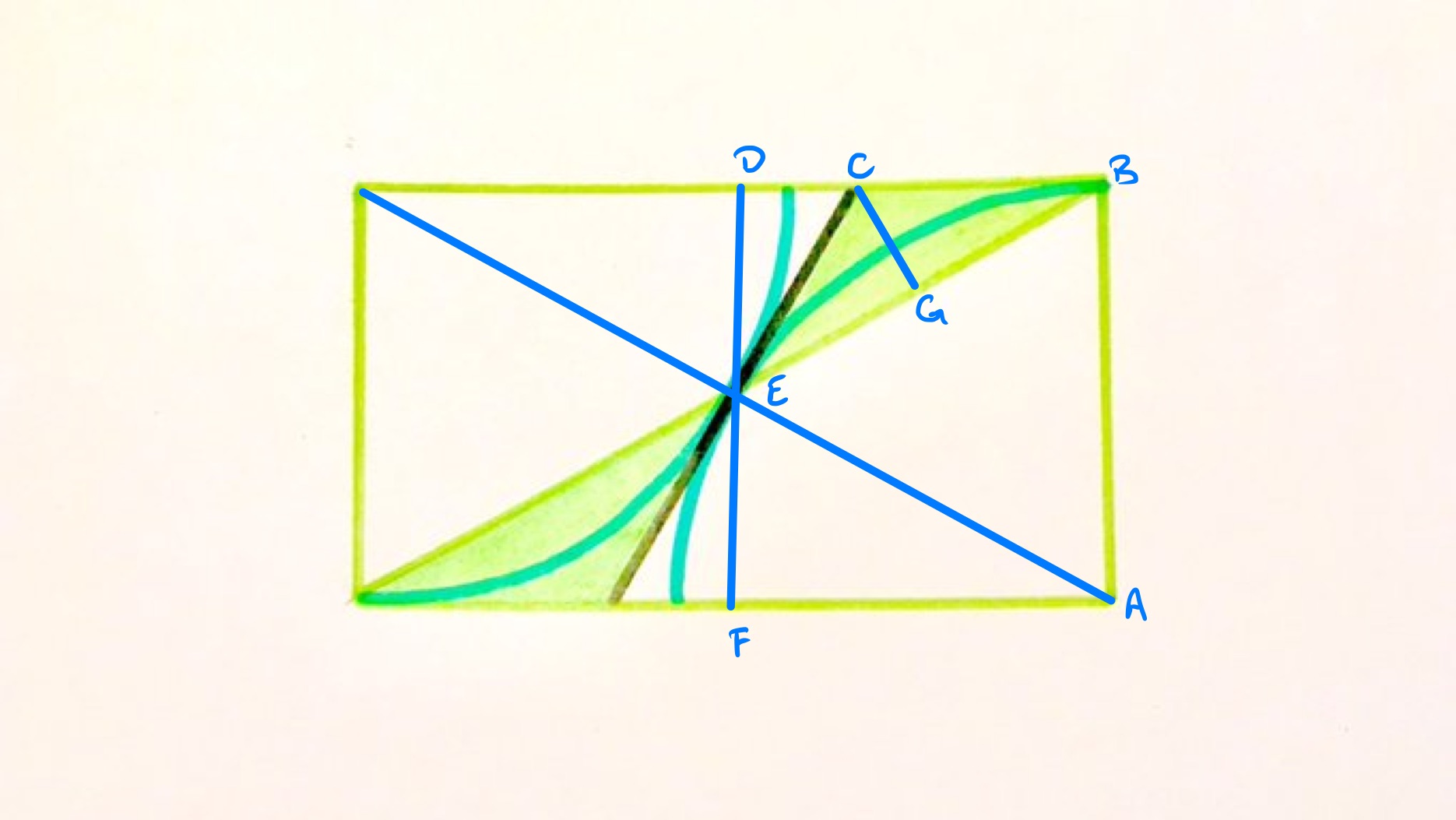
With the point labelled as above, line segments $A E$ and $B E$ are both half-diagonals so have the same length. Since $E$ and $B$ lie on a circle centred at $A$, $A E$ and $A B$ have the same length. Therefore, triangle $A E B$ is equilateral. Triangle $E B D$ is then half an equilateral triangle of the same size, and the area of the whole rectangle is the same as four of these equilateral triangles.

Since the angle between a radius and tangent is $90^\circ$, angle $G \hat{E} C$ is $90^\circ - 60^\circ = 30^\circ$ and so triangle $B C E$ is isosceles. Point $G$ is the midpoint of $E B$, and so triangles $C G B$ and $C G E$ are congruent. Since $C D E$ is also a right-angled triangle with angle $30^\circ$ at vertex $E$, it is also congruent to triangle $C G E$, so the area of triangle $B C E$ is two thirds of that of $E B D$.

Putting all of that together, the area of the shaded region is two thirds of that of the equilateral triangle $A E B$ and so is one sixth of the area of the full rectangle.