Notes
quarter circles in a rectangle in a circle solution
Quarter Circles in a Rectangle in a Circle
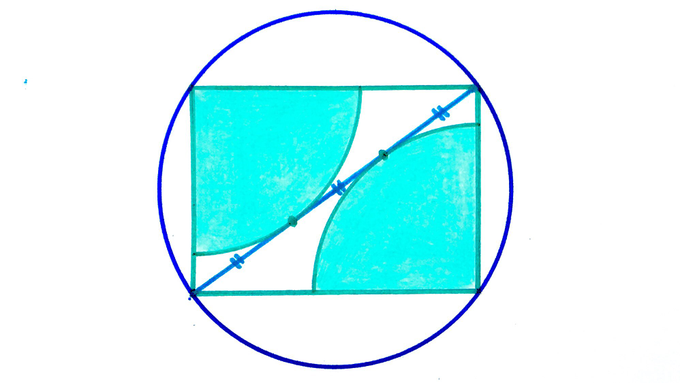
What fraction is shaded?
Solution by Similar Triangles, Angle in a Semi-Circle, and Angle Between a Radius and Tangent
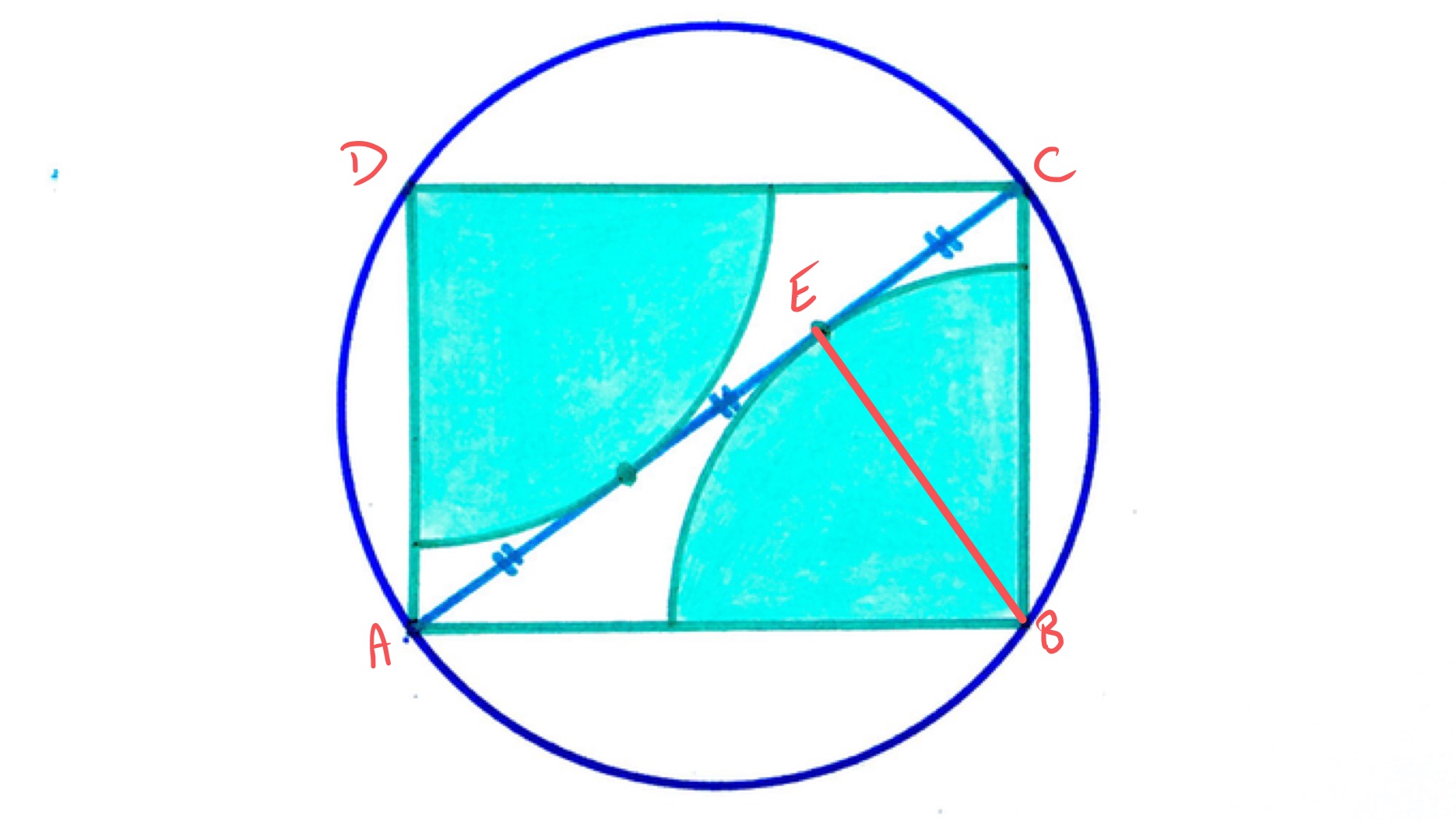
With the points labelled as above, is a radius of the quarter circle and a tangent where the radius meets the circle, so angle is the angle between a radius and tangent so is a right-angle. This means that triangles and are similar, with corresponding to .
Let be the length of , so that is the radius of the quarter circle, and let be the length of , so that has length . Then as and are similar, the ratio is equal to which means that .
As angle is a right-angle, and the angle in a semi-circle is a right-angle, is a diameter of the larger circle. Its radius is therefore .
The area of the larger circle is then and of the two quarter circles is . Therefore the fraction that is shaded is .