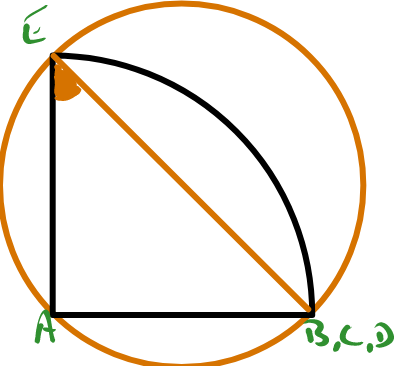Notes
quarter circle overlapping a circle solution

Solution to the Quarter Circle Overlapping a Circle Problem

Using Angles in a Circle

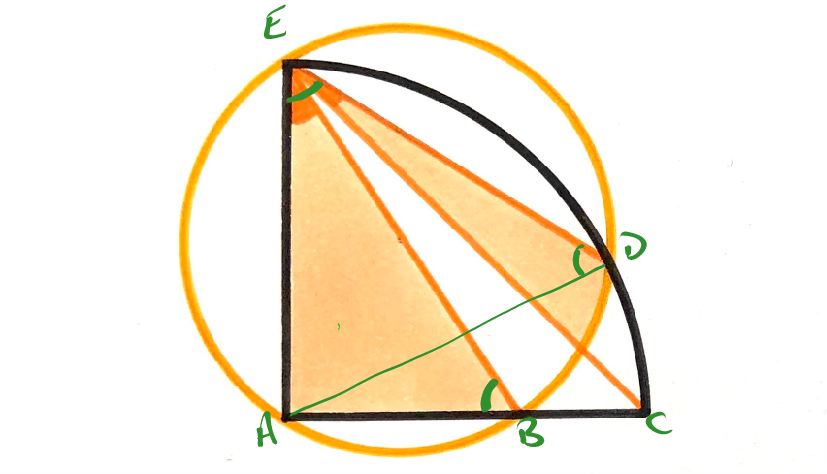
Using the labels from the above diagram, the total angle that we want to calculate can be written as:

Now, angles $A \hat{B } E$ and $A \hat{D } E$ are the same because they are subtended at the orange circle from the same chord. Then angles $A \hat{D } E$ and $A \hat{E } D$ are the same because triangle $A D E$ is isosceles as sides $A D$ and $A E$ are both radii of the black quarter circle.

Since triangle $A B E$ is a right angled triangle, $A \hat { E } B + A \hat { E } D = 90^\circ$. Since triangle $A C E$ is isosceles, angle $A \hat{ E } C = 45^\circ$. Combining these, we get:

Using the Invariance Principle

In this problem, the size of the orange circle can change so we can invoke the Agg invariance principle. As it varies, the location of point $B$ (in the above diagram) slides between $A$ and $C$. By sliding it to $C$, the angle $A \hat{ E } B$ becomes $45^\circ$ while the other two angles become zero.