Notes
quadrilateral splitting a semi-circle solution
Quadrilateral Splitting a Semi-Circle
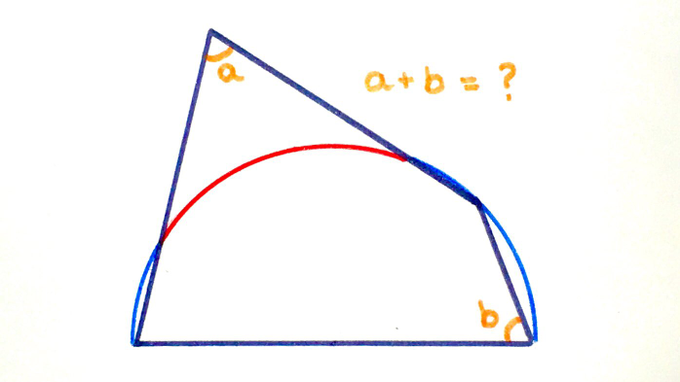
In total, the blue arcs have the same length as the red. What’s the sum of these two angles?
Solution by Cyclic Quadrilateral, Angle at the Centre is Twice the Angle at the Circumference, Angles in a Triangle, and Angles on a Straight Line
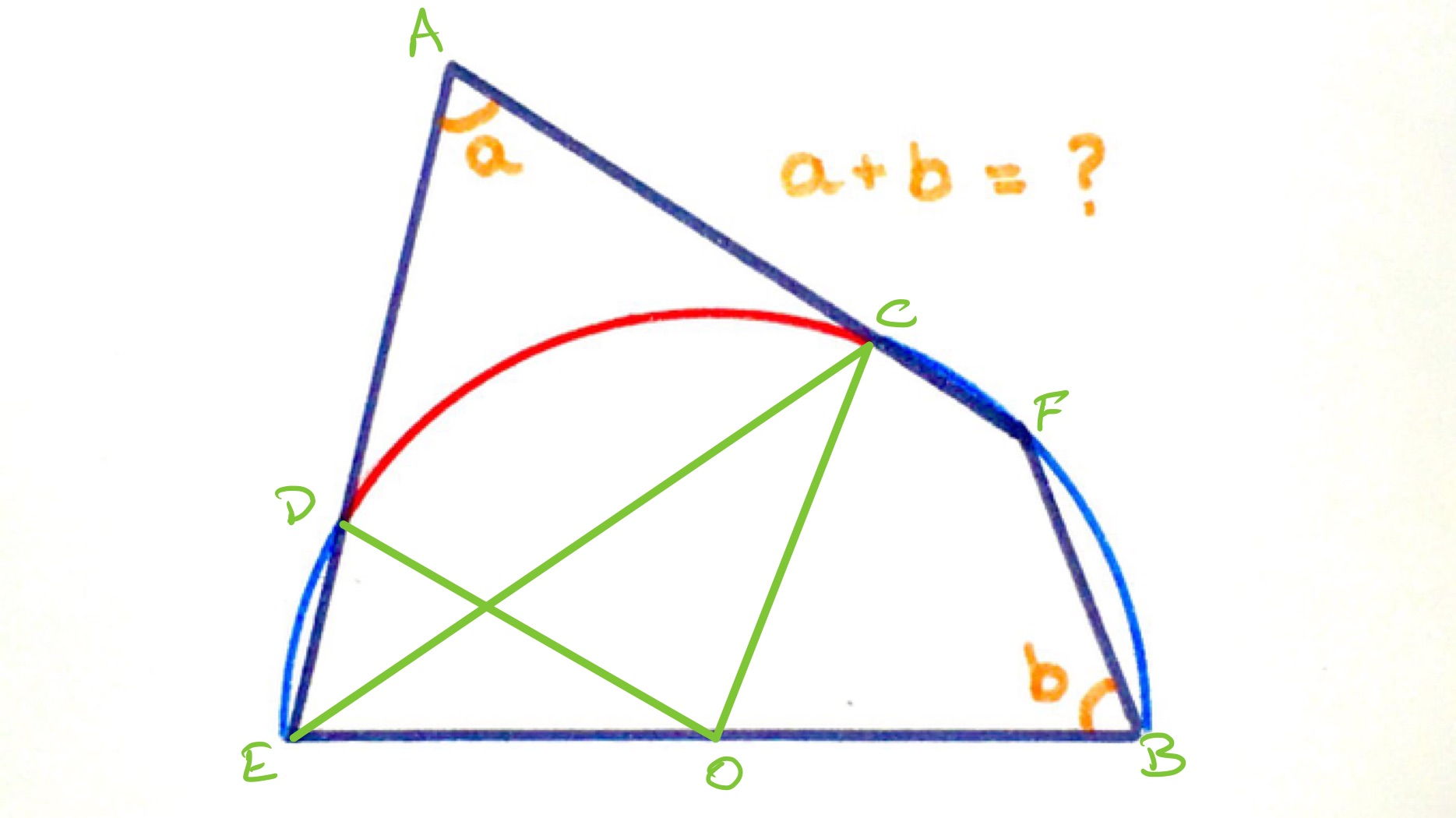
In the above diagram, quadrilateral is cyclic and so angles and add up to . Then as angles at a point on a straight line also add up to , angle is equal to angle , which is .
As the blue arcs have the same length as the red, the red arc is half a semi-circle and so the angle is . Using the fact that the angle at the centre is twice the angle at the circumference, this establishes angle as .
Since angles in a triangle add up to , from triangle then and so .
Solution by Invariance Principle
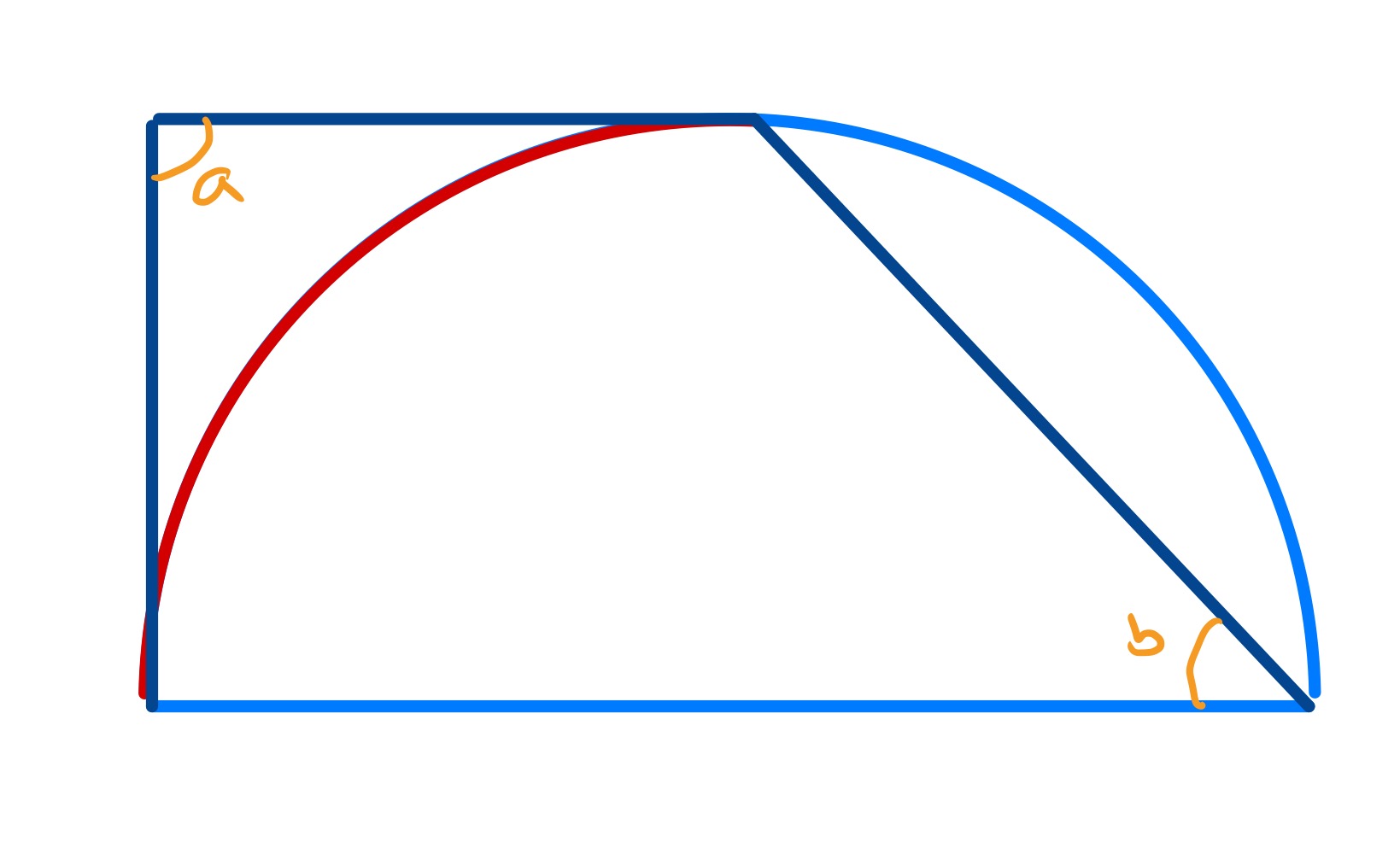
In this version of the diagram, angle is and angle is so their sum is .
There is another version of the diagram in which the red arc is centrally placed in the semi-circle and where point coincides with point . In this diagram, angle can be calculated as , but it appears that angle is which does not give the expected answer. However, by taking to the same place as , the angle should now be thought of as the tangential angle at which is . As this is not a trivial step, this doesn’t fully qualify as a solution by invariance principle as the purpose of such solutions is to make the answer more obvious.