Notes
pentagram in a circle solution
Pentagram in a Circle
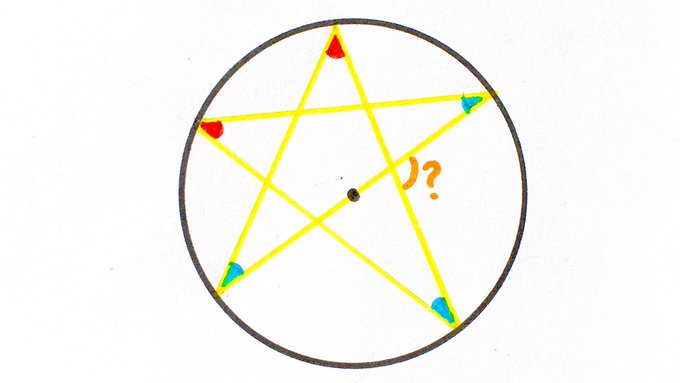
Angles of the same colour are the same size. What’s the orange angle?
Solution by Angles in a Semi-Circle, Angles in the Same Segment, and Angles in a Triangle
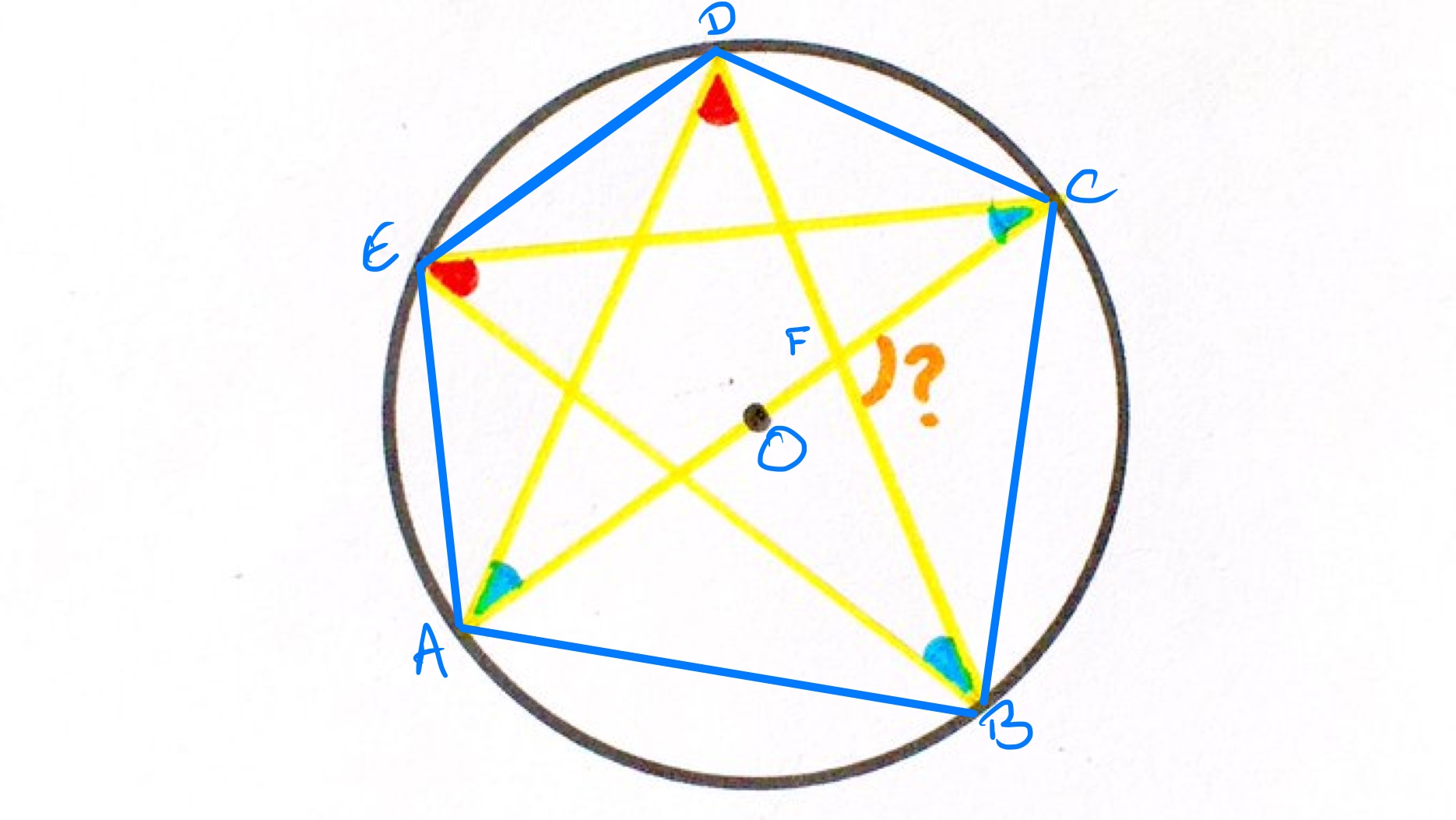
With the points labelled as in the diagram, the line segment is a diameter of the circle. Since the angle in a semi-circle is a right-angle, angles , , and are all . Then as angles in the same segment are equal, angle is the same as angle . This means that the red angle is . Also, angles and are the same so as angles in a triangle add up to , considering triangle shows that the blue angle is .
Again, using angles in the same segment then angle is the same as , which is , and angle is the same as , which is . So as angles in a triangle add up to , angle is .