Notes
partitioned square solution

Solution to the Partitioned Square Puzzle

Solution by Similar Triangles, Area of a Triangle and Square, and Pythagoras' Theorem

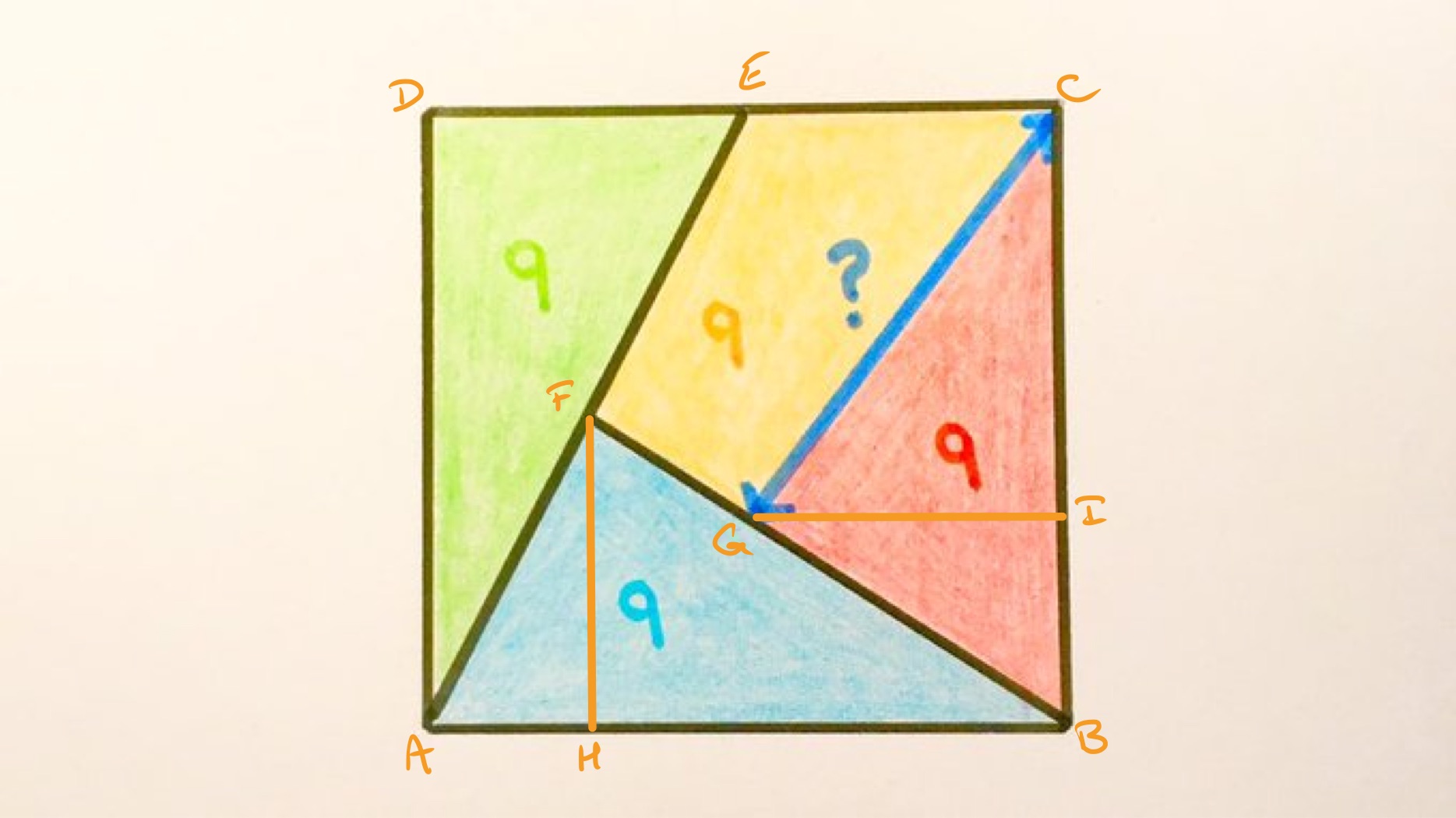
The area of the full square is $4 \times 9 = 36$, so its side length is $6$. Considering triangle $A D E$, it has area $9$ so applying the area of a triangle then the length of $D E$ must be $3$. Similarly, the lengths of $H F$ and $I G$ are also $3$.

Triangle $A H F$ is similar to triangle $E D A$, so as $H F$ is half the length of $D A$, $A H$ is half the length of $D E$, namely $\frac{3}{2}$. Therefore $H B$ has length $\frac{9}{2}$. Similarly, triangle $G I B$ is similar to $B H F$, and the ratio of the lengths of $H B$ to $G I$ is $\frac{9}{2} : 3$, so as $B I$ corresponds to $H F$ it has length $3 \div \frac{9}{2} \times 3 = 2$.

Therefore $C I$ has length $6 - 2 = 4$, and so triangle $C I G$ is a right-angled triangle with shorter sides $3$ and $4$. Its hypotenuse, which is $C G$, therefore has length $5$ by Pythagoras' theorem.