Notes
parallelogram area solution
Parallelogram Area
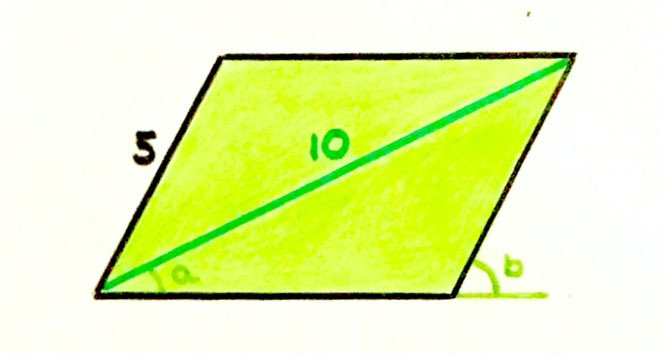
is a right angle. What’s the area of the parallelogram?
Solution by Similar Triangles and Pythagoras' Theorem
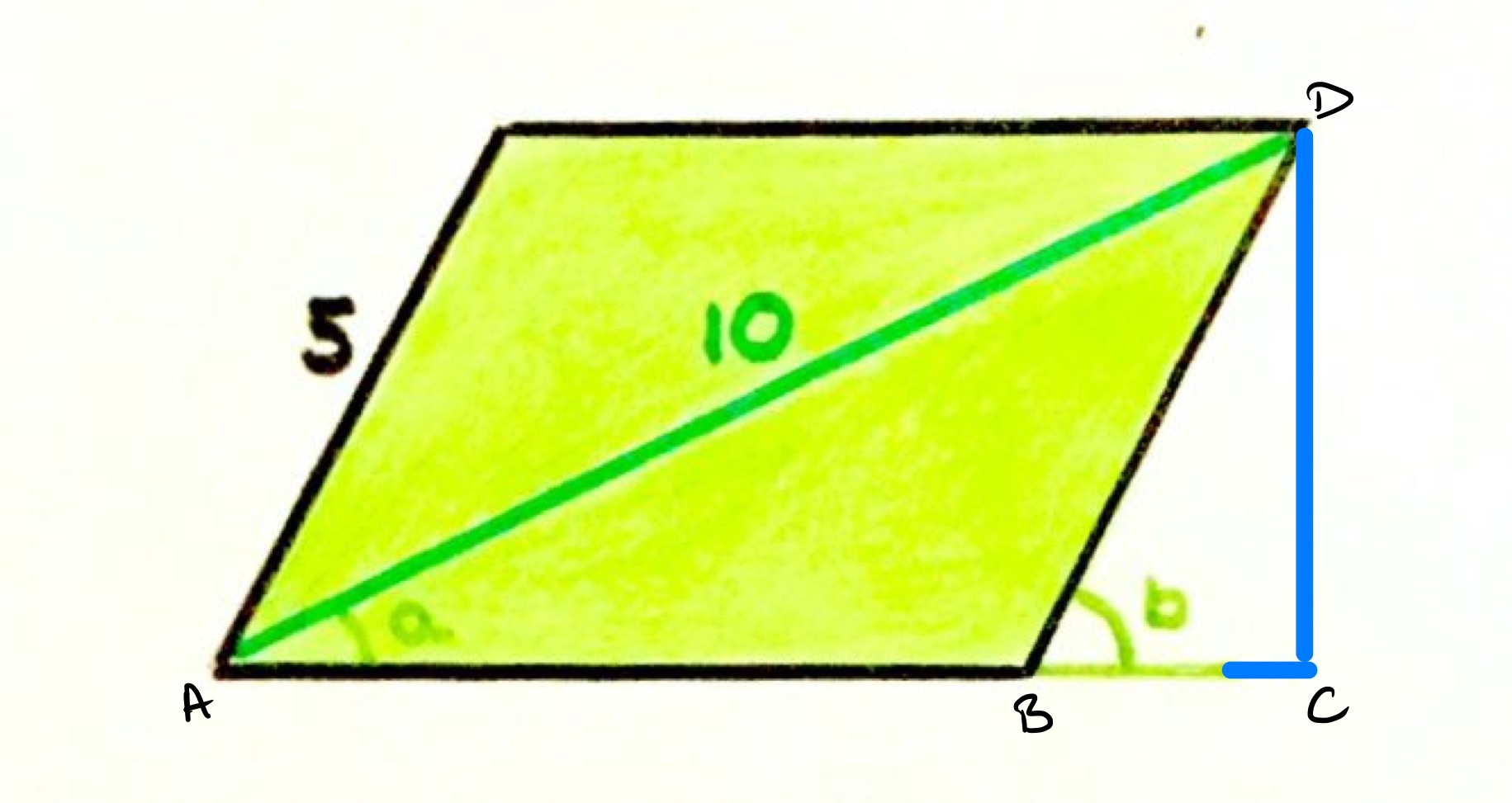
In the diagram above point is on the continuation of so that angle is a right-angle. Since angles in a triangle add up to , angle is therefore which is . Triangle is also a right-angled triangle with angle and so triangles and are similar. Since has length and has length , triangle is double triangle .
Let be the length of . Then has length and has length , so has length . The area of the parallelogram is then . Applying Pythagoras' theorem to triangle yields the equation:
and so . Therefore, the area is .