Notes
overlapping triangles in a circle solution
Solution to the Overlapping Triangles in a Circle Puzzle
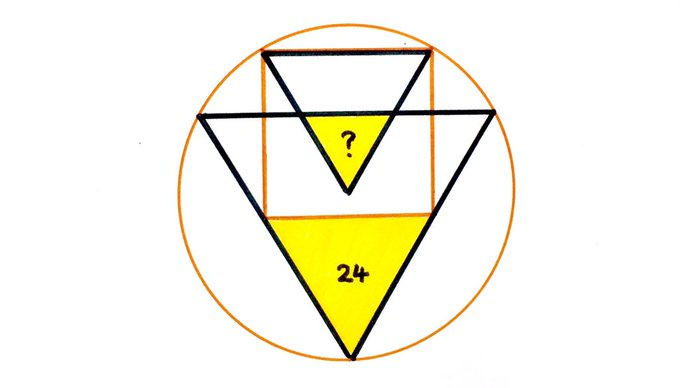
The circle contains a square and two overlapping equilateral triangles. What’s the area of this overlap?
Solution by Angle at the Centre is Twice the Angle at the Circumference, Isosceles and Equilateral Triangles
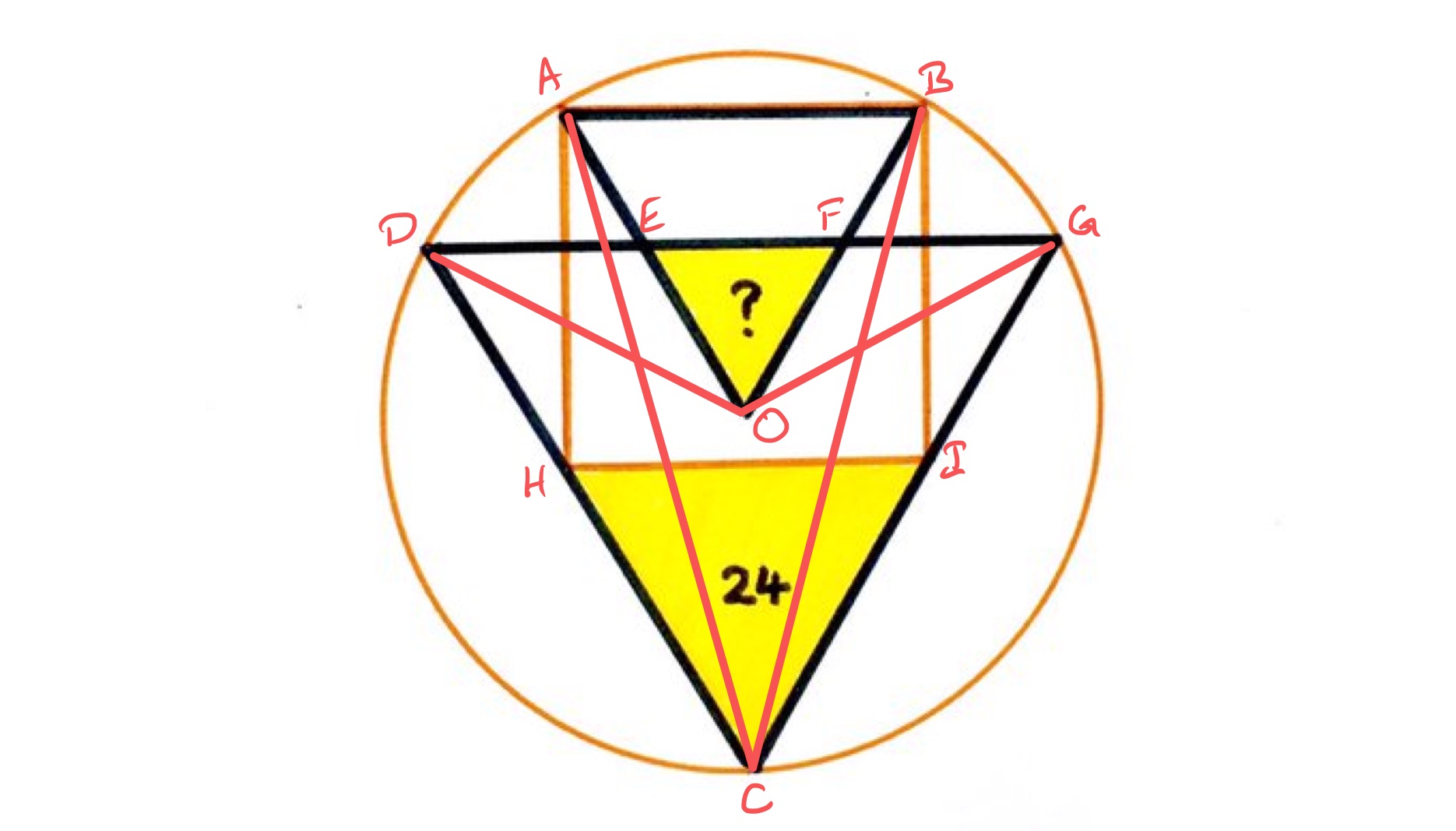
Let the points be labelled as above.
Consider triangle . As is a square and an equilateral triangle, and have the same length so triangle is isosceles. Angle is so angle is . A similar argument shows that angle is also , so angle is . This is half of angle so as triangle is equilateral, since the angle at the centre is twice the angle at the circumference, is the centre of the circle.
Triangle is then isosceles with angle at (as it is twice angle ). This means that angle is which is the same as angle so triangle is isosceles and can be thought of as two half equilateral triangles aligned along their short sides. The length of is therefore times the length of .
Then is the same length as , and of , and of . So the side length of equilateral triangle is times the side length of . The area of is therefore times the area of , and so has area .