Notes
one rectangle inside another with semi-circles solution
Solution to the One Rectangle Inside Another With Semi-Circles Puzzle
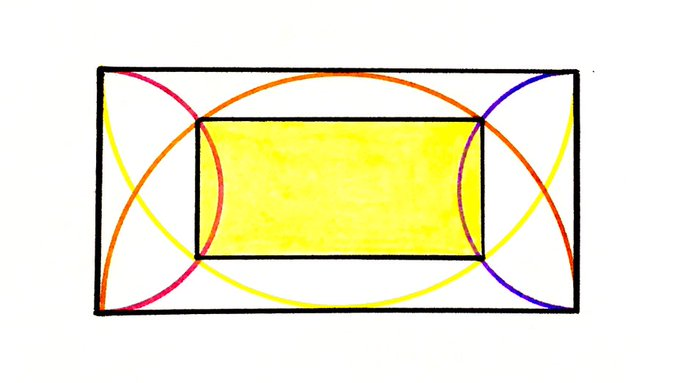
What fraction of the outer rectangle is shaded?
Solution by Pythagoras' Theorem
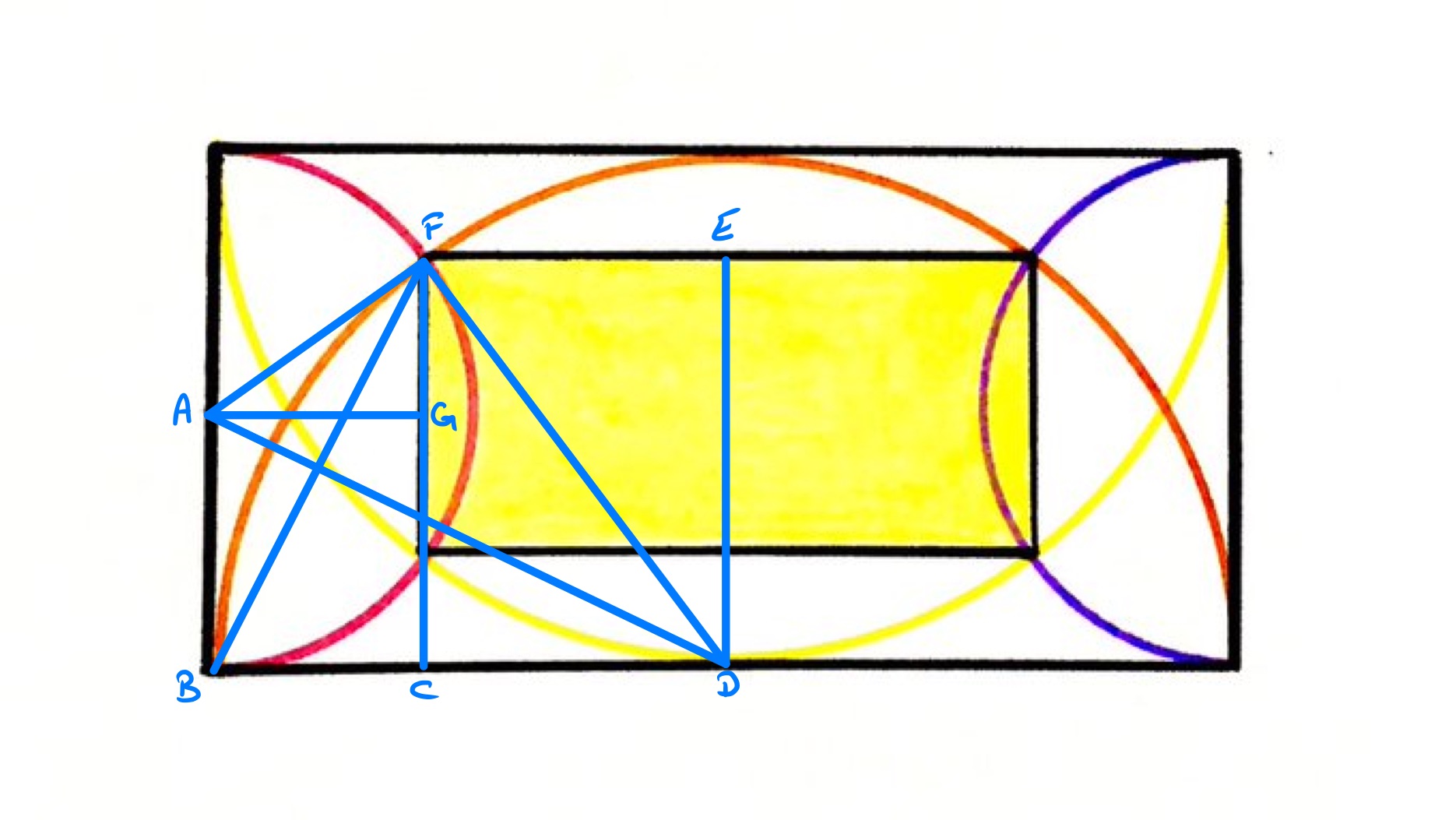
With the points as labelled above, let be the length of and of . Let be the radius of the smaller semi-circles, then is the radius of the larger ones.
Triangle is right-angled with lengths , , and . Applying Pythagoras' theorem gives the identity:
So .
Triangle is also right-angled with lengths , , . Applying Pythagoras' theorem gives the identity:
So .
Putting these together shows that . Substituting back into the second then shows that so and then . The dimensions of the yellow rectangle can therefore be computed as and . The area of the yellow rectangle is then while the area of the outer rectangle is . Therefore the fraction that is shaded is .