Notes
nested semi-circles solution
Nested Semi-Circles
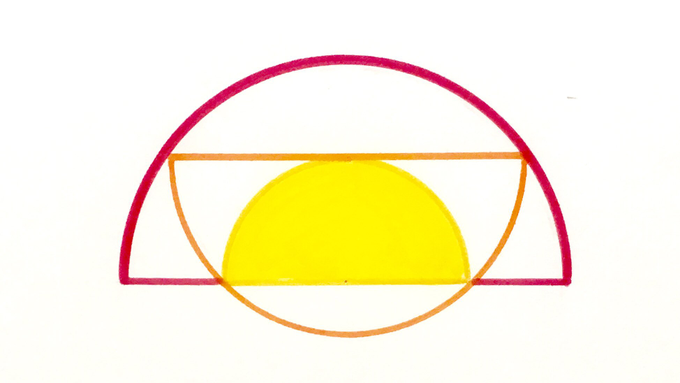
What fraction of the largest semicircle is shaded?
Solution by Chord Properties and Pythagoras' Theorem
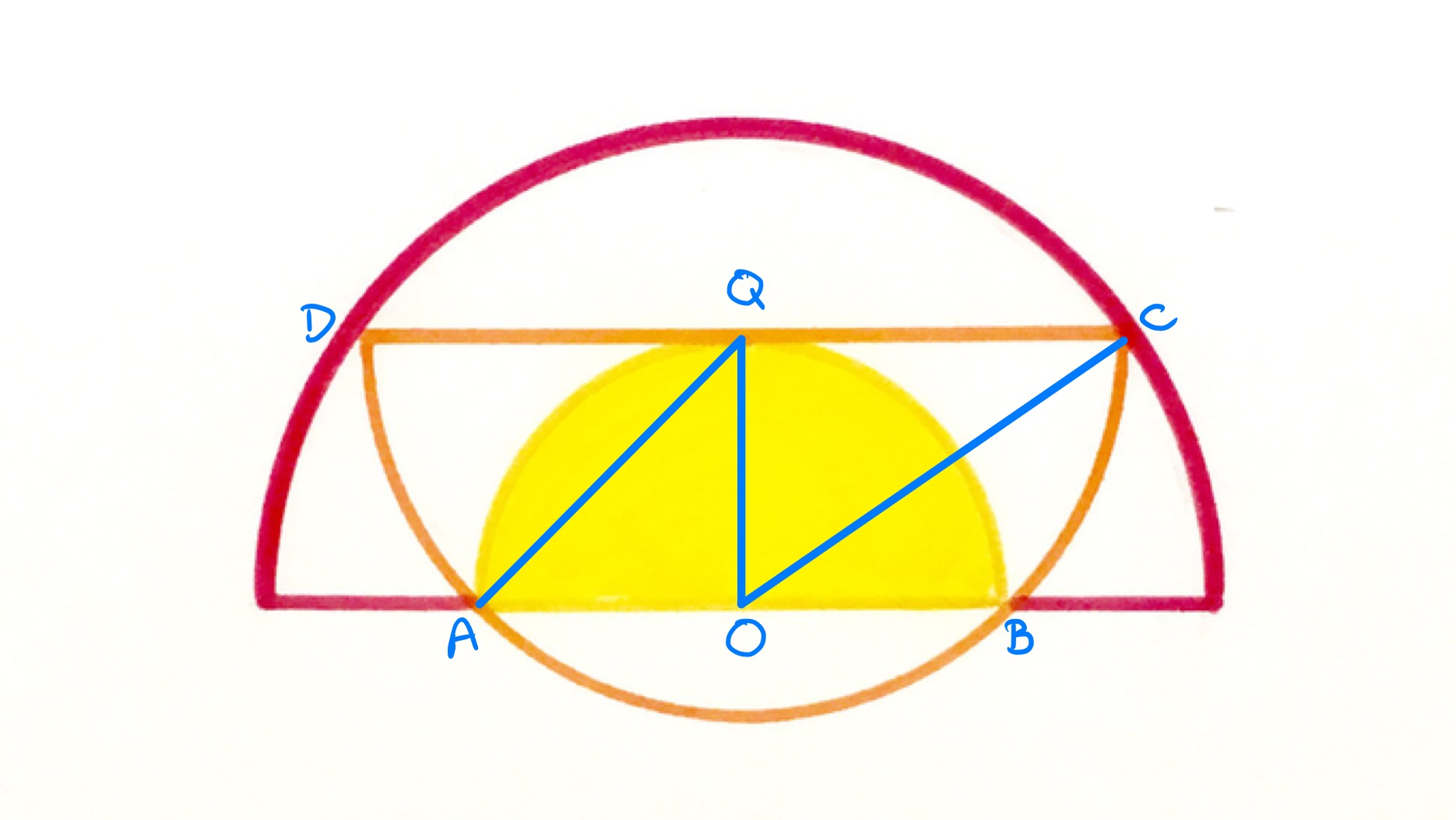
In the above diagram, is the midpoint of and so is the centre of the smallest semi-circle while is the midpoint of and so is the centre of the middle semi-circle.
As is a chord of the middle semi-circle, the perpendicular bisector of passes through its centre. That bisector passes through the midpoint, which is , and so is perpendicular to . The line segment is tangential to the smallest circle and so is perpendicular to since the angle between a radius and tangent is a right angle. This means that is also the perpendicular bisector of and so is also the centre of the largest semi-circle.
Let , , be the radii of the three semi-circles in increasing order. Applying Pythagoras' theorem to triangle shows that . Applying it to triangle shows that .
The area of the largest semi-circle is therefore times that of the smallest, so of the largest is shaded.