Notes
nested isosceles triangles solution
Nested Isosceles Triangles
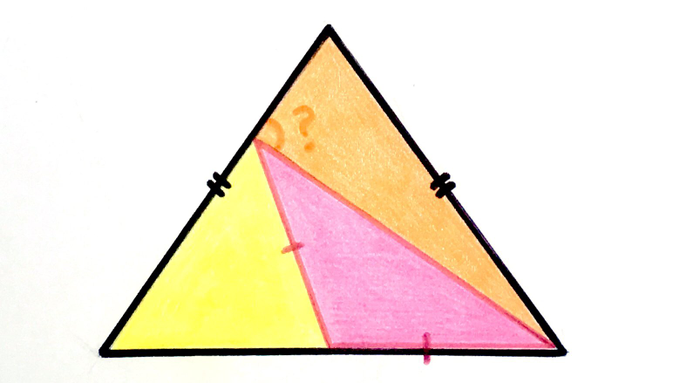
Both the outer black triangle and inner pink triangle are isosceles, and the three coloured areas are equal. What’s the angle?
Solution by Triangle area, Angle in a Semi-Circle, and Angles on a Straight Line
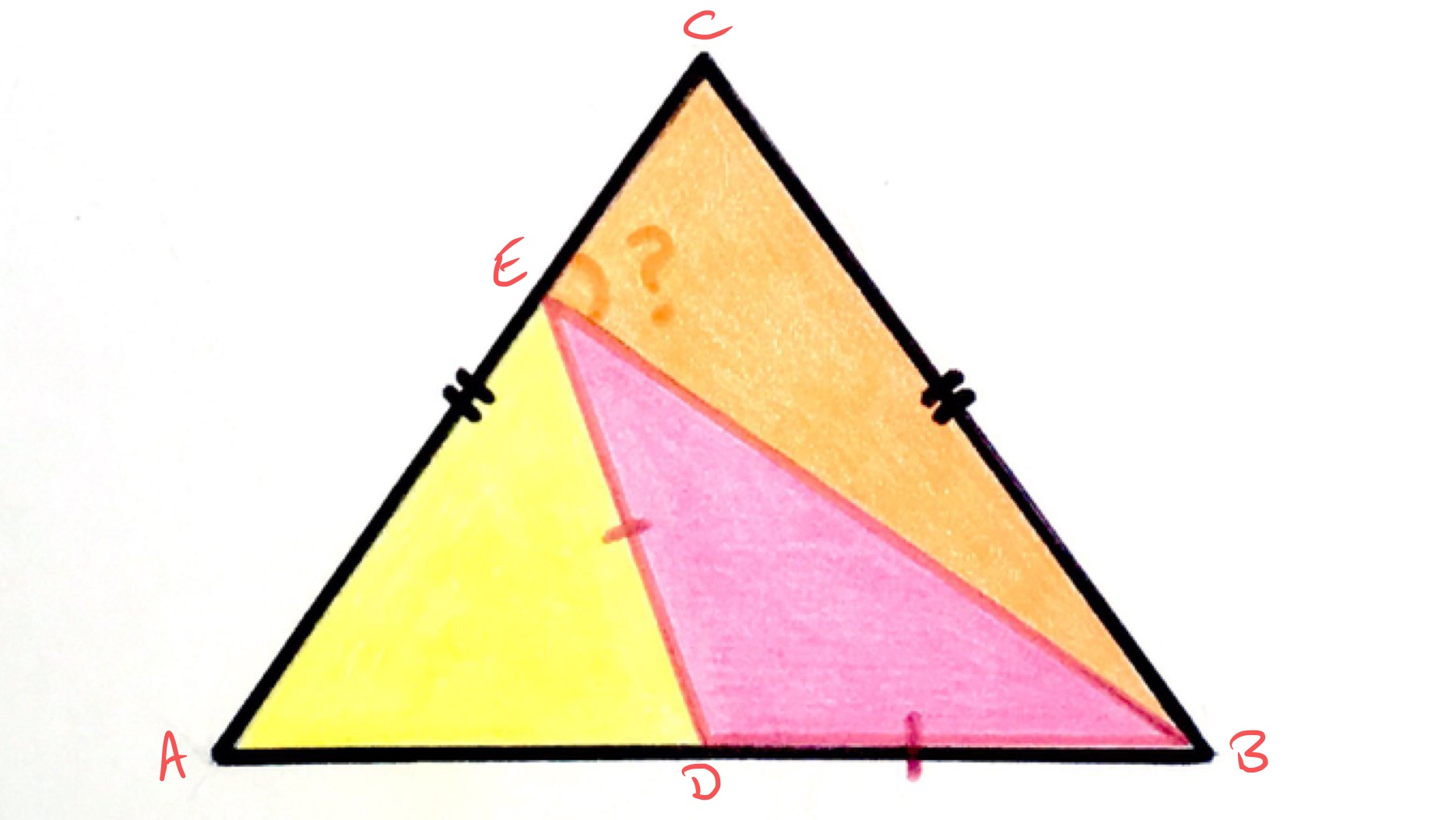
With the points labelled as in the above diagram, triangles and have the same area and the same height above the line , so the lengths of their bases along that line must be the same. That is, and have the same length. So a circle centred on that passes through will also pass through and . The line segment is then a diameter of that circle and a point on its circumference, so since the angle in a semi-circle is , angle is . Then as angles at a point on a straight line add up to , angle is also .