Notes
nested circles and a triangle solution
Nested Circles and a Triangle
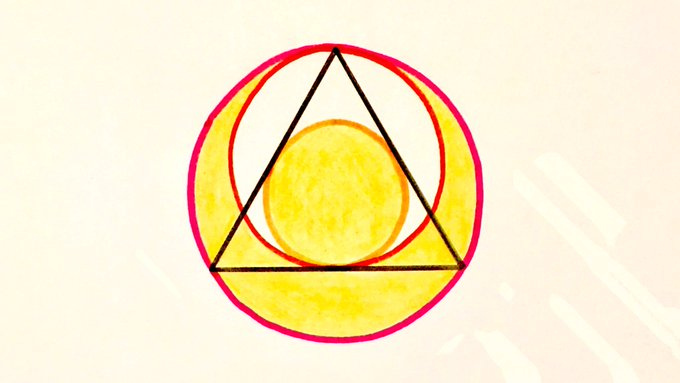
What fraction is shaded? The triangle is equilateral.
Solution by Lengths in an Equilateral Triangle
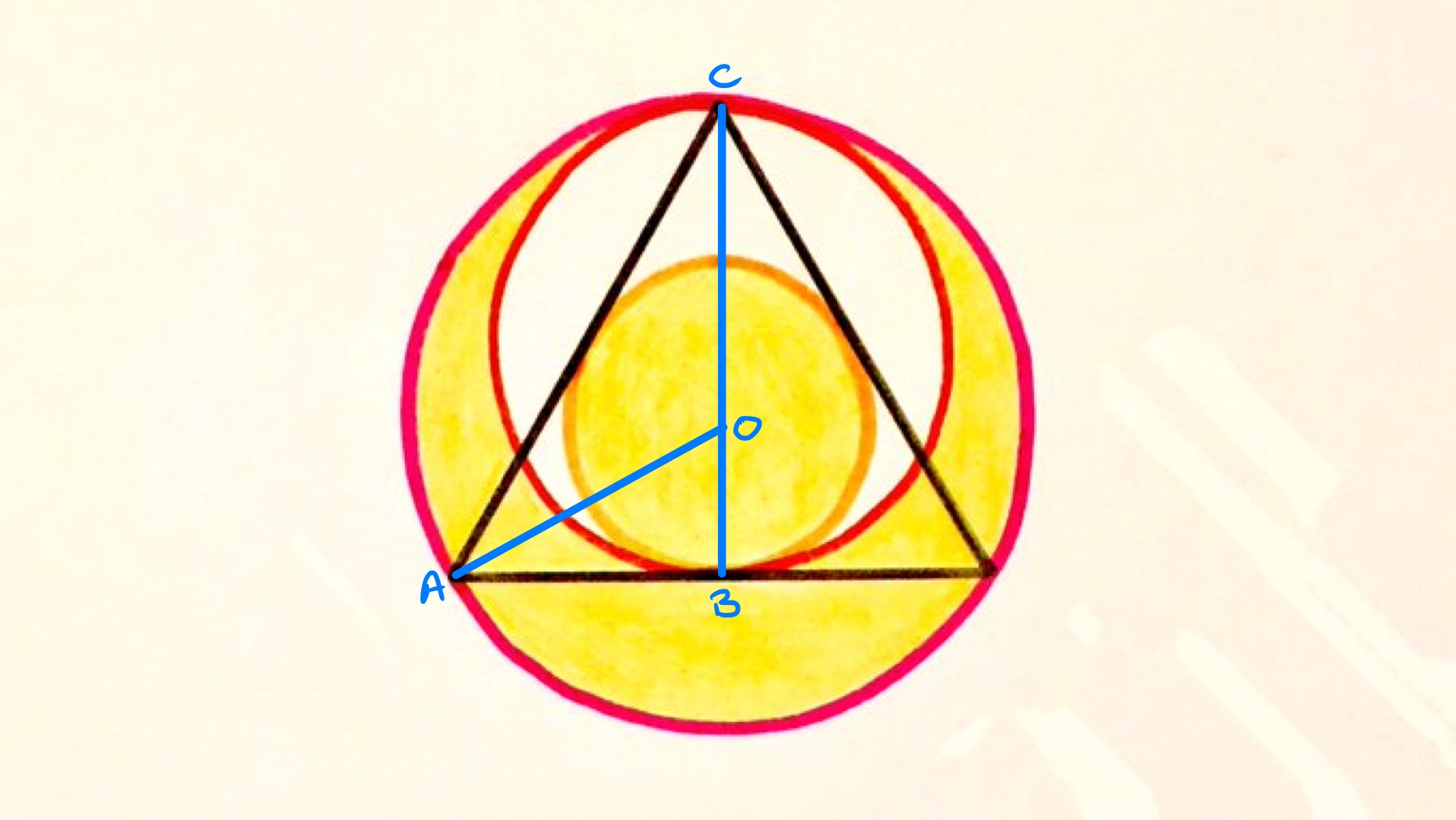
In the above diagram, is a radius of the smallest circle, of the largest circle, and is a diameter of the middle circle. Since is also a radius of the largest circle, the length of is the sum of the lengths of and .
From considering the lengths in an equilateral triangle, has half the length of and so is one third of the length of . Let be the length of , then has length and the radius of the middle circle is . The shaded region then has area:
The area of the outer circle is so the fraction that is shaded is .