Notes
multiple semi-circles in a circle solution

Solution to the Multiple Semi-Circles in a Circle Puzzle

Solution by Area of a Circle

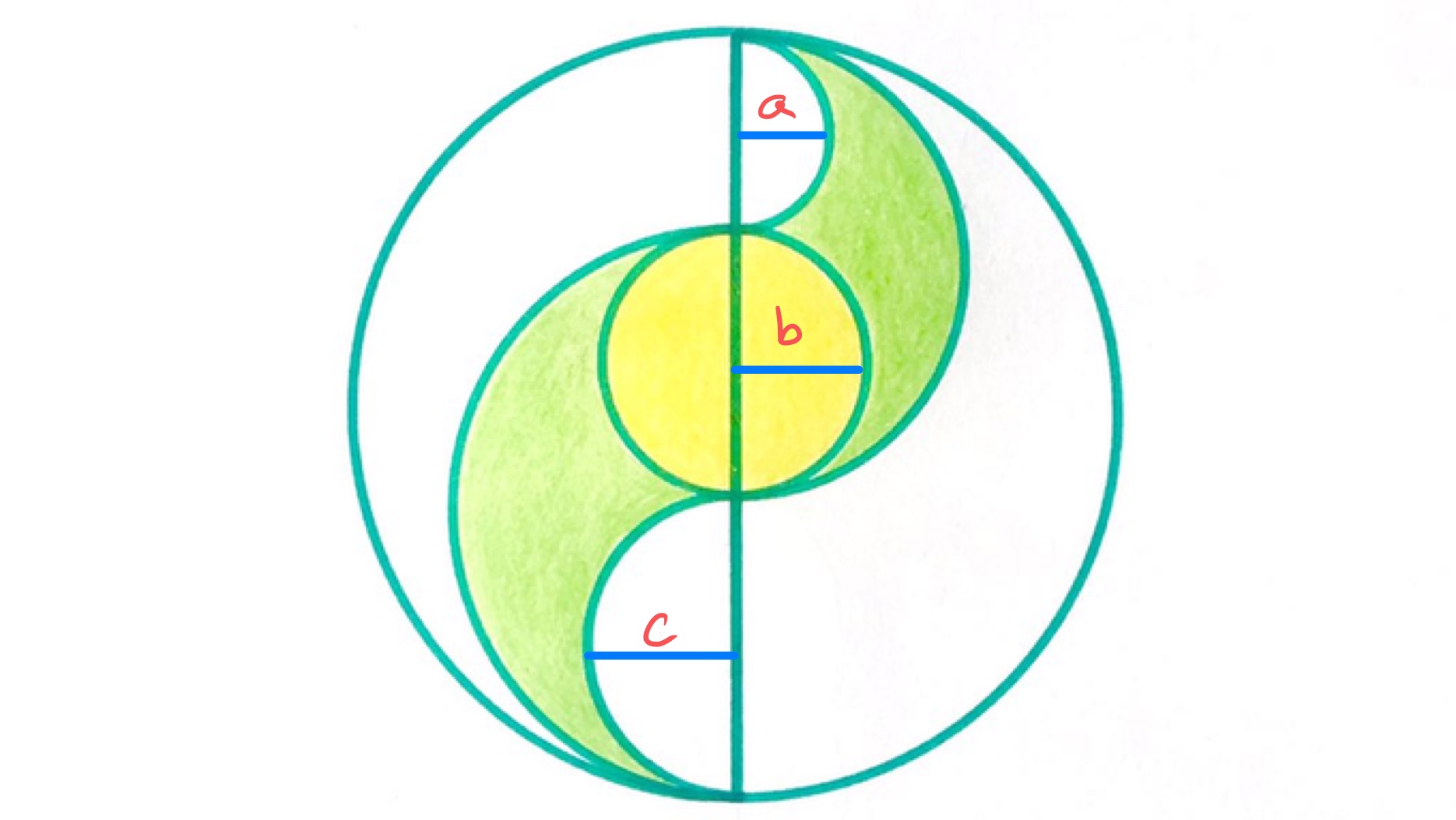
As in the diagram, let $a$, $b$, and $c$ be the radii of the three smallest circles. The upper green circle has radius $a + b$, the lower green radius $b + c$, and the full circle has radius $a + b + c$.

The area of the upper green region is:

Likewise, the area of the lower green region is $\pi b c$. The total green area is thus $\pi b (a + c)$. This is double the yellow area, which is $\pi b^2$, so $a + c = 2 b$ and the total shaded area is $3 \pi b^2$.

As $a + c = 2 b$, the radius of the outer circle is $3 b$ and so its area is $9 \pi b^2$. The fraction of this that is shaded is therefore $\frac{1}{3}$.