Notes
multiple semi-circles iii solution
Solution to the Multiple Semi-Circles III Puzzle
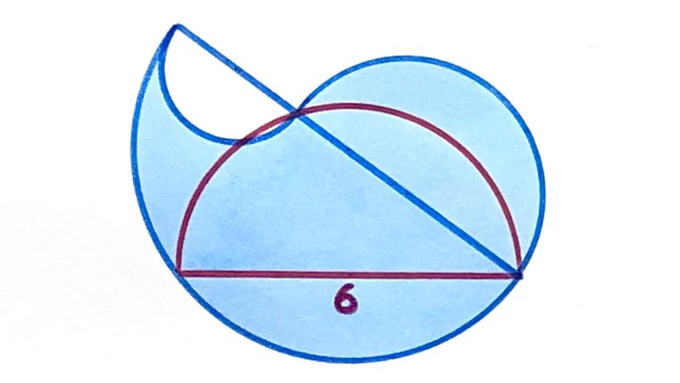
The red diameter is . What’s the total shaded area?
Solution by Circle Areas and Similar Triangles
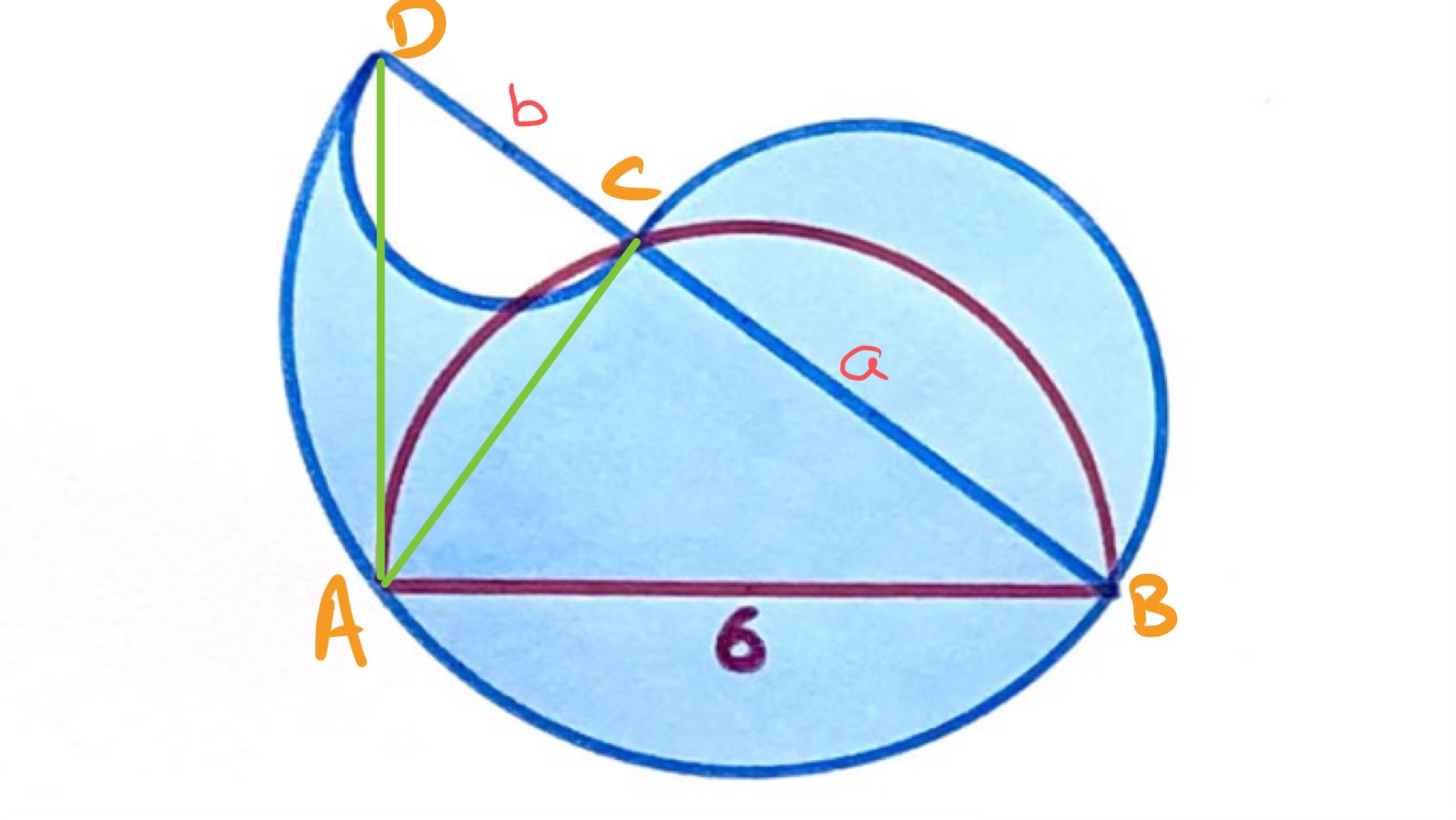
With the edges labelled as above, the largest semi-circle has area , and the other two have areas and . The shaded area therefore has area:
The triangles and are similar, with corresponding to and to , so . Hence . Rearranging this yields so the shaded area is .
The use of similar triangles can be replaced by Pythagoras' Theorem. Writing for the length of and for the length of , the various right-angled triangles imply the following identities:
Putting this together,
so
Substituting this into the expression for the shaded area gives that that area is as before.
Solution by Invariance Principle
The point can slide on the red semi-circle. As it approaches then the diagram gets very large, but putting it at produces a diagram that makes the solution obvious.
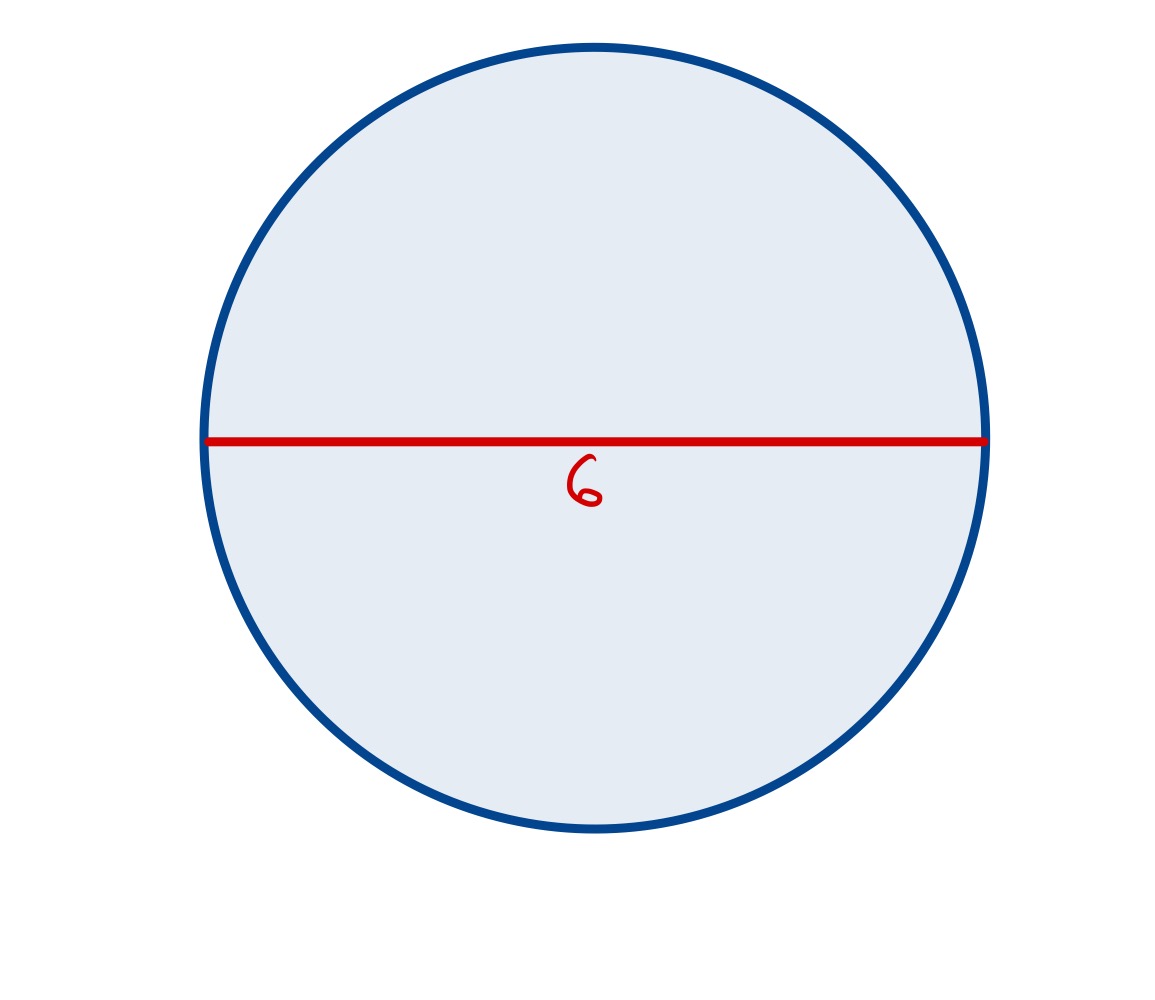
The radius of the circle is so its area is .