Notes
multiple angles solution
Solution to the Multiple Angles Puzzle
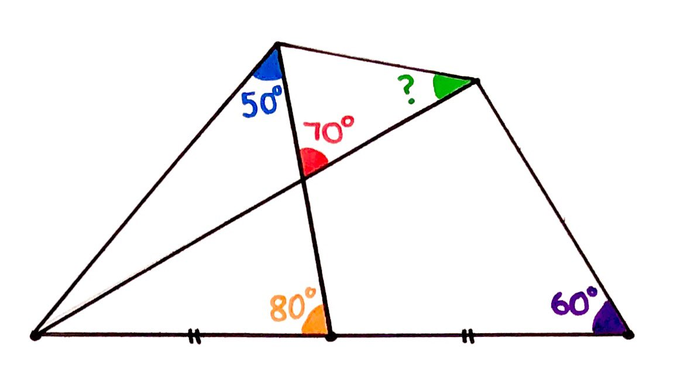
What’s the angle?
Solution by Angles in a Triangle
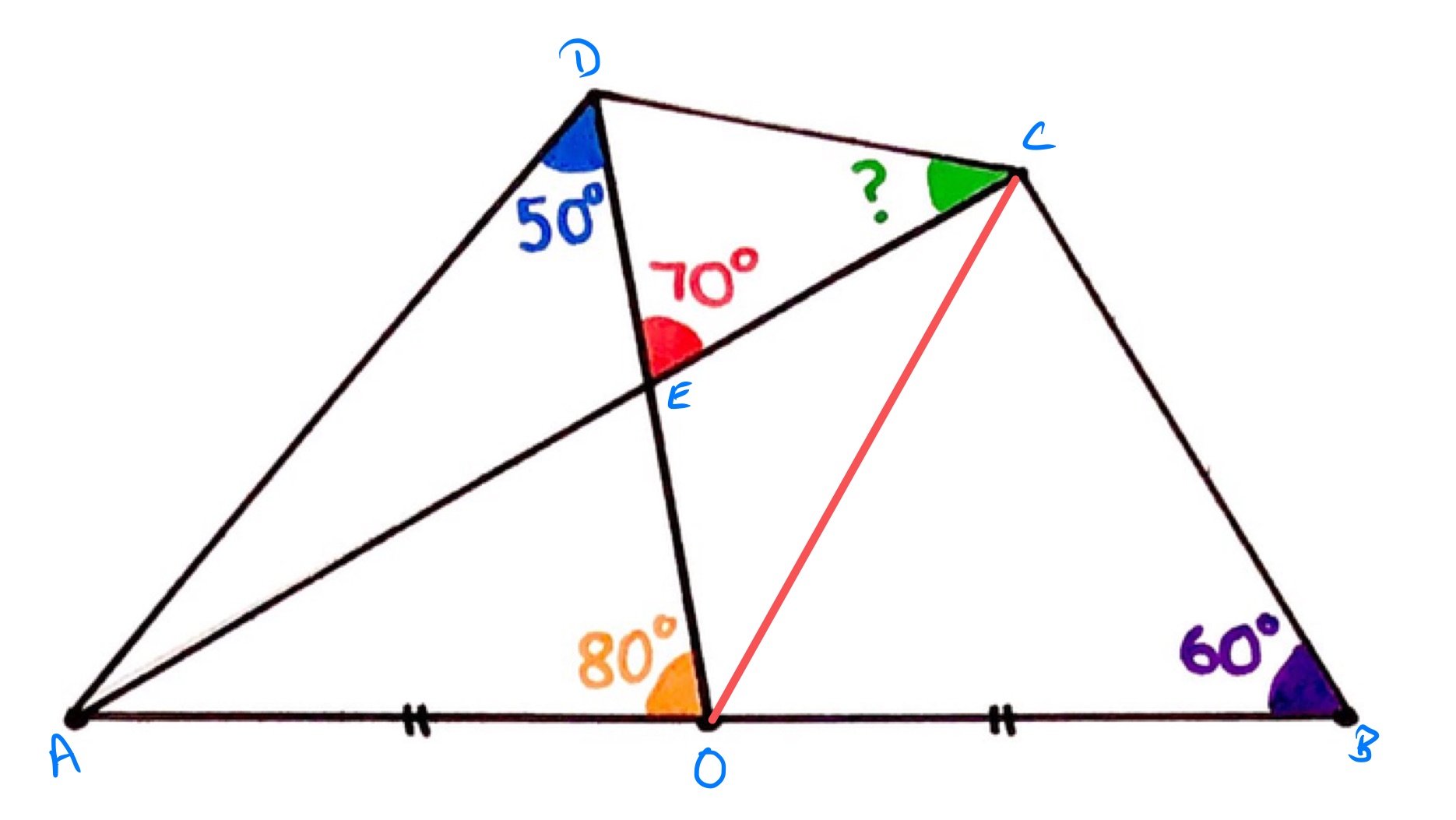
The angles at can be filled in using angles at a point on a line add up to , so angle , , and .
Using the fact that angles in a triangle add up to , various other angles can be now be filled in.
From triangle , angle is . This means that triangle is isosceles, and so the length of is the same as that of .
From triangle , angle is . Then from triangle , angle is .
The point is the midpoint of , so as triangle is a right-angled triangle, joining to results in two isosceles triangles. That is, has the same length as and .
Since triangle is isosceles, and angle is , triangle is actually equilateral. This means that angle is . So angle is as angles at a point on a line add up to .
Both and are equal to , so triangle is also isosceles. As angle is , angle is .
Finally, from triangle , angle is .
Solution by Angle in a Semi-Circle and Angles in the Same Segment
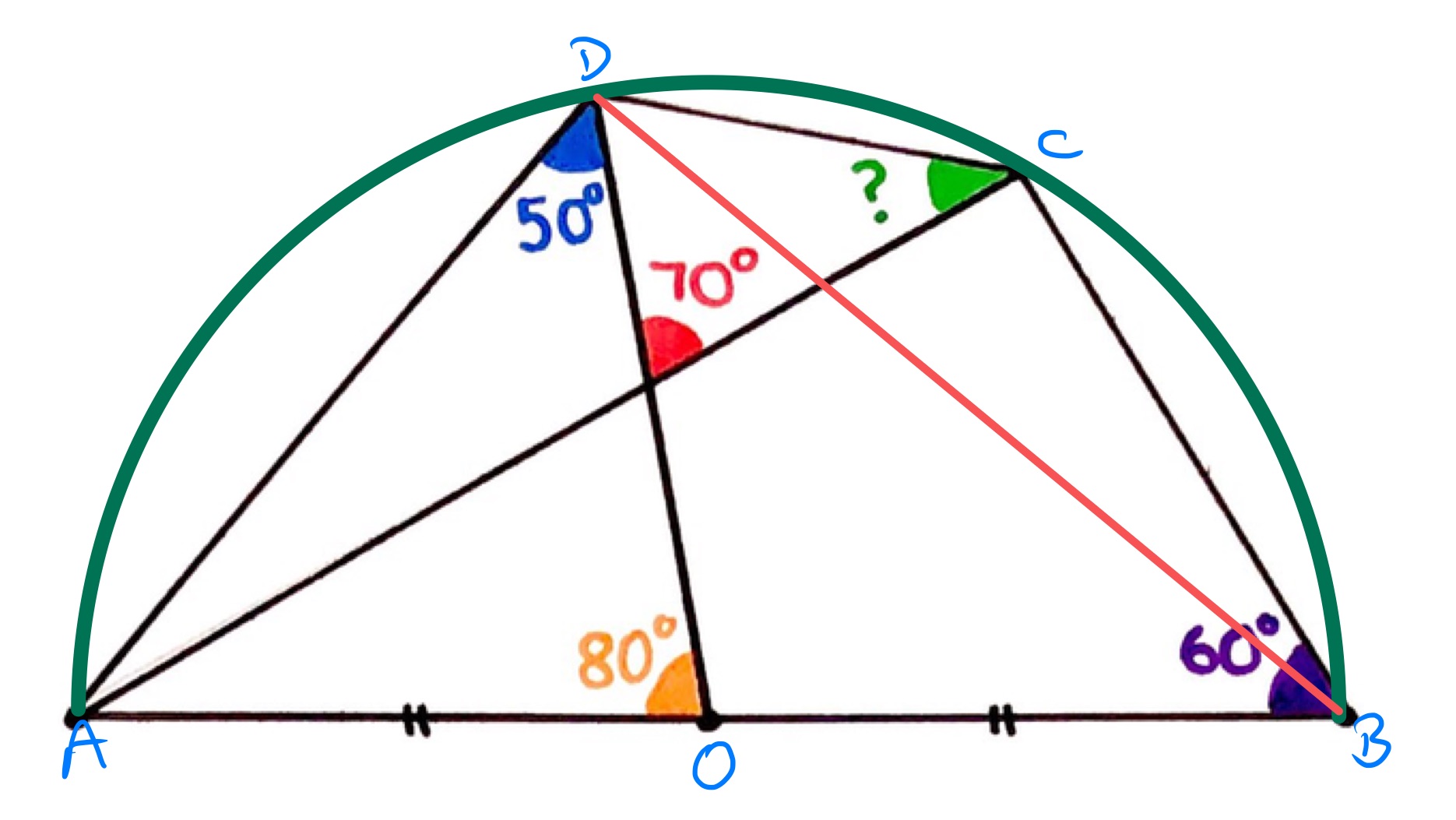
In the above diagram, the semi-circle is centred on with diameter .
Angle is since angles in a triangle add up to , so triangle is isosceles. Therefore is the same length as and so lies on the semi-circle.
Angle is since vertically opposite angles are equal, so angle is . Angle is therefore and so as angle in a semi-circle is , is also on the semi-circle.
Angles and are equal as they are angles in the same segment. Triangle is a right-angled triangle and angle is so angle . Hence the green angle is .