Notes
lengths in a crossed trapezium solution
Lengths in a Crossed Trapezium
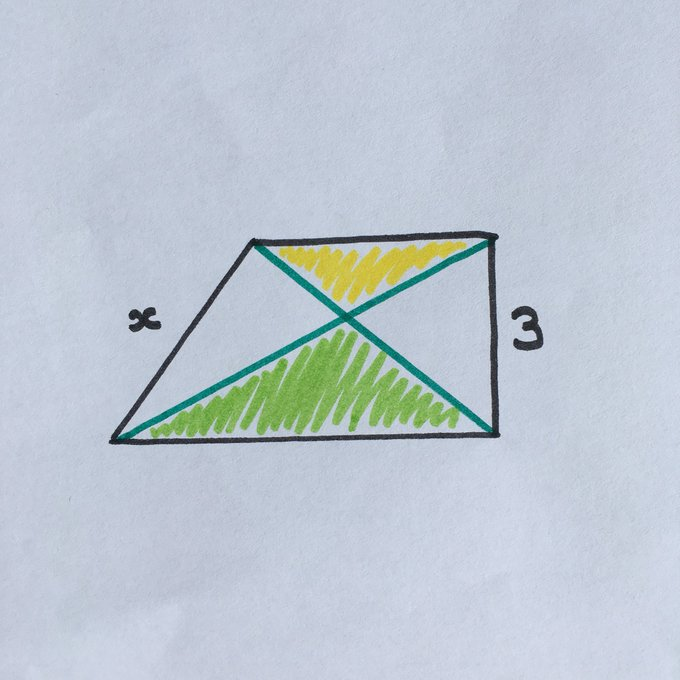
In this right-angled trapezium, the green area is more than the yellow area. What’s the length of the sloping side?
Solution by Similar Triangles and Pythagoras' Theorem
LengthsinaCrossedTrapeziumLabelled.png
In the above diagram, let and be the lengths of the parallel sides in the trapezium, so that has length and has length . Triangles and are similar, so and are in the ratio . Since has length , this means that has length and has length .
The area of triangle is and of is so:
Therefore .
Applying Pythagoras' theorem to triangle then shows that
and so .