Notes
hexagon and a square solution
Solution to the Puzzle
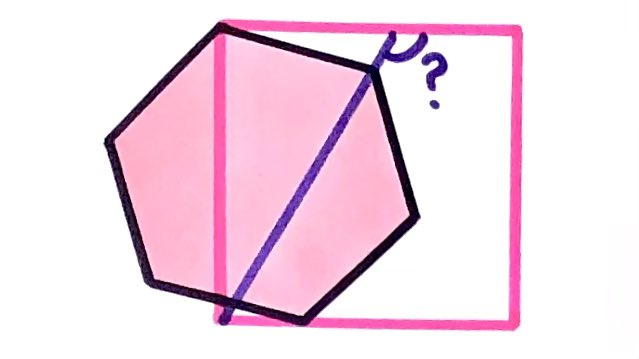
A regular hexagon and a square. What’s the angle?
Solution by Transformations
For this solution, take the origin to be the upper left corner of the square. We focus on two points, the opposite vertex of the hexagon, , and the vertex lying on the slanted line, .
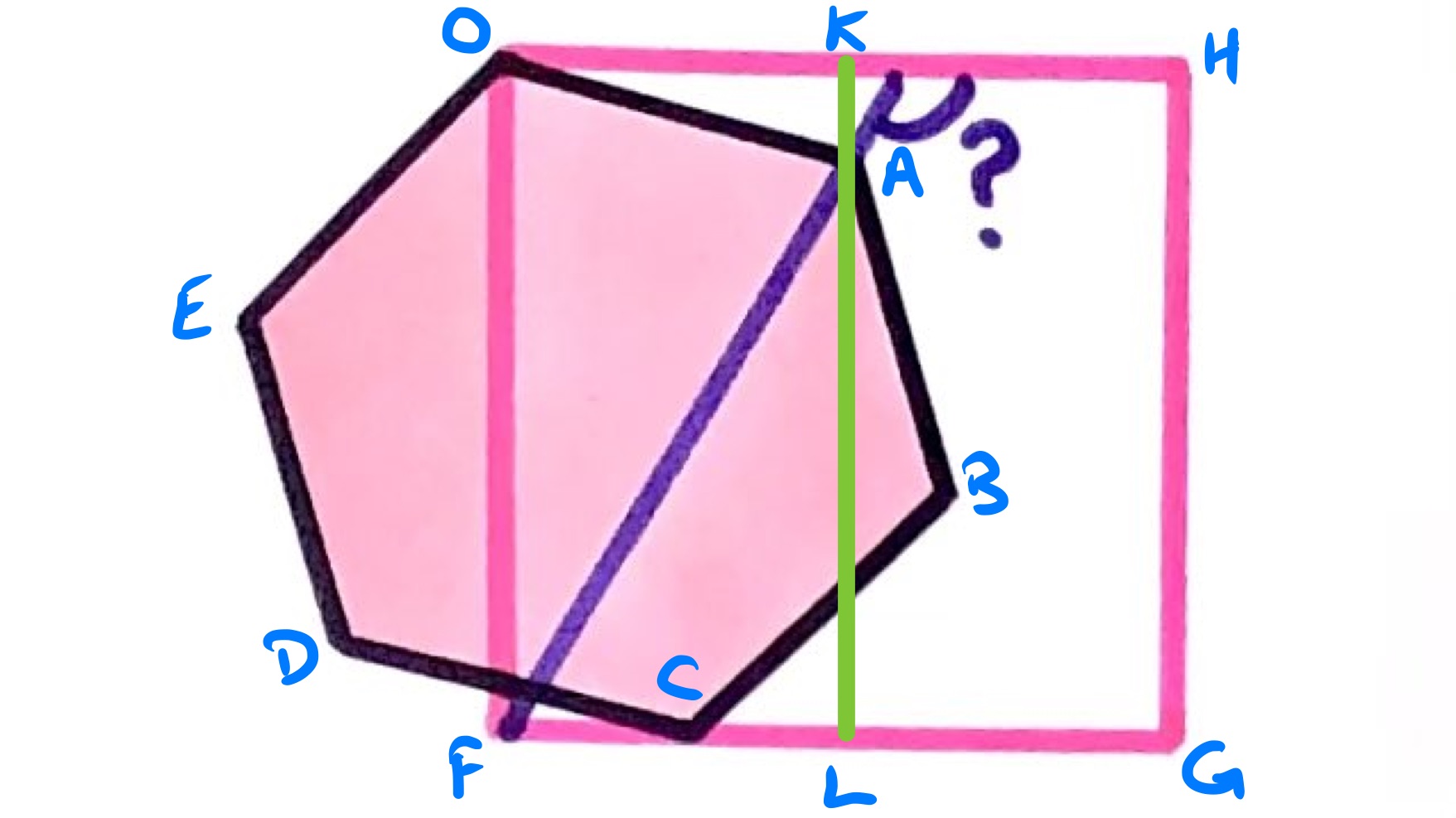
With respect to the origin, the point is obtained from by scaling by a factor of and then rotating anti-clockwise by . This is irrespective of where actually resides and is due to the structure of the hexagon.
The point is constrained to move on the line segment that runs from to , and as it does so moves on a line obtained by applying these transformations to and since these transformations preserve lines.
As the original line is horizontal, the transformed line is at to the horizontal, and so the marked angle is .
Solution by Similar Triangles
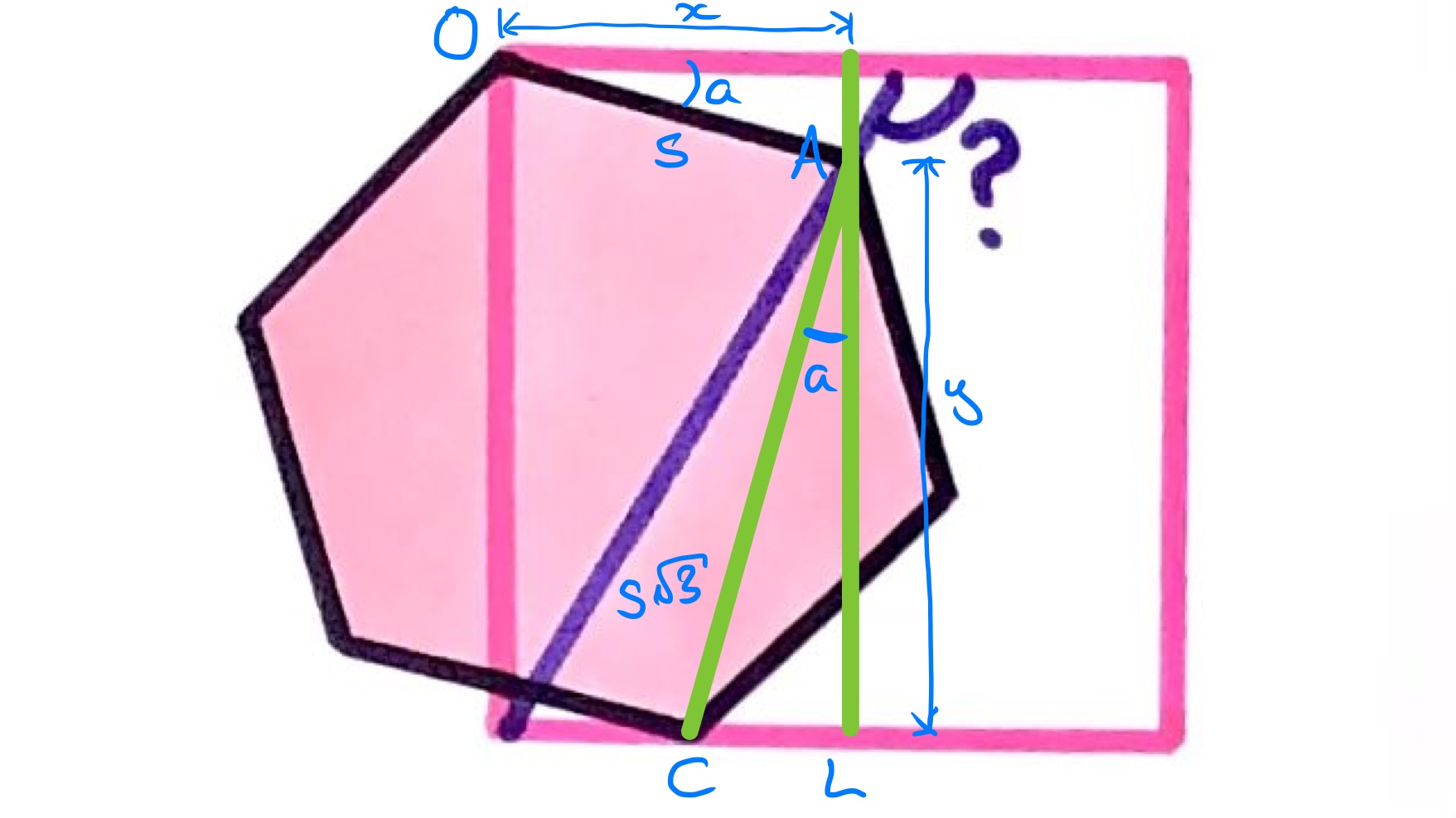
Using the labelled version above, the gradient of the purple line can be found by taking the displacement of point from point . The horizontal displacement is the distance , which is the adjacent side to the angle in triangle . The vertical displacement is the distance which is adjacent to the angle in triangle . These two triangles are similar, and the two sides correspond, so their quotient is the scale factor between them. The hypotenuse of the smaller is the side length of the hexagon, while the hypotenuse of the larger is the vertical “height” of a hexagon when resting on a side. The scale factor is therefore and so this is the gradient of the line .
A line with gradient is at to the horizontal, so the marked angle is .
Solution by the Invariance Principles
We can apply both the Strong and Weak invariance principles to this problem. The property that can be varied is the angle at which the hexagon is tilted with respect to the square.
To apply the strong version we consider either of the extremes for this angle. At one extreme the top edge of the hexagon lies along the top edge of the square and the purple line is a diagonal of the hexagon, whereupon the angle we are looking for is half an interior angle plus an exterior angle, thus . At the other extreme, the hexagon is tilted so that the vertical side of the square forms a diagonal. The purple line then cuts an equilateral triangle in half so makes an angle of with the vertical, and thus with the horizontal.
To apply the weak version, as the angle is unique the purple line must be fixed and so the vertex must be constrained to move on it. Thus if we can show that that vertex is constrained to move in a straight line (as seen from the bottom left vertex of the square) then we are (almost) done.