Notes
four stacked squares in a circle in a square solution
Four Stacked Squares in a Circle in a Square
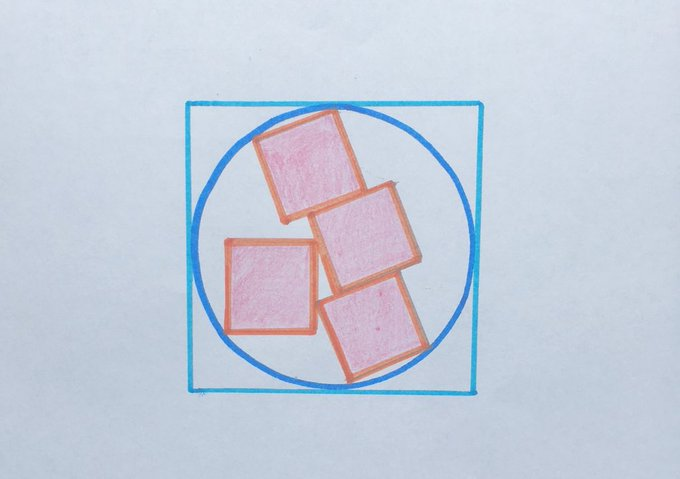
What fraction of the big square is shaded? Shaded squares are identical.
Solution by Angle in a Semi-Circle and Pythagoras' Theorem
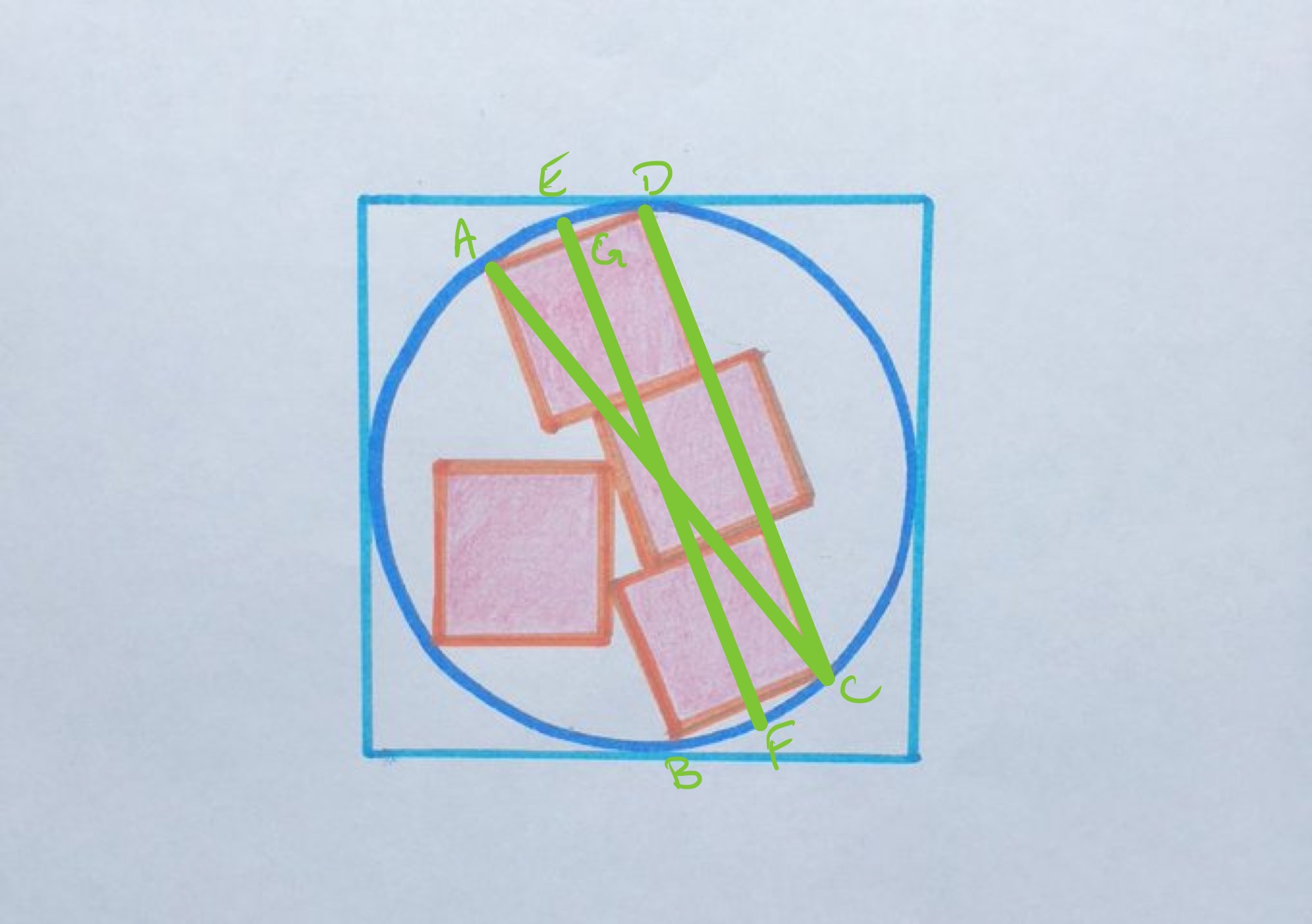
The line segments and are parallel, so their perpendicular bisectors are also parallel. As both are chords, the centre lies on both of them, and so these perpendicular bisectors are actually the same line. As the line segments are of equal length, the line segment is then parallel to this perpendicular bisector. Triangle is then a right-angled triangle and so is a diameter since the angle in a semi-circle is a right-angle.
Let be the length of a side of a small square and let be the side length of the large square. Then has length and the diameter of the circle is . Applying Pythagoras' theorem shows that:
Therefore one small square is one tenth of the large square, so ths of the large square is shaded.
Solution by Intersecting Chords Theorem
With and as above, and have length , has length and has length . Applying the intersecting chords theorem gives
Which gives the fraction shaded as as before. and the same length, and are both chords of the circle. The perpendicular bisectors of both pass through the centre of the circle, and since the chords are parallel the perpendicular bisectors are also parallel.