Notes
four squares viii solution
Solution to the Four Squares VIII Puzzle
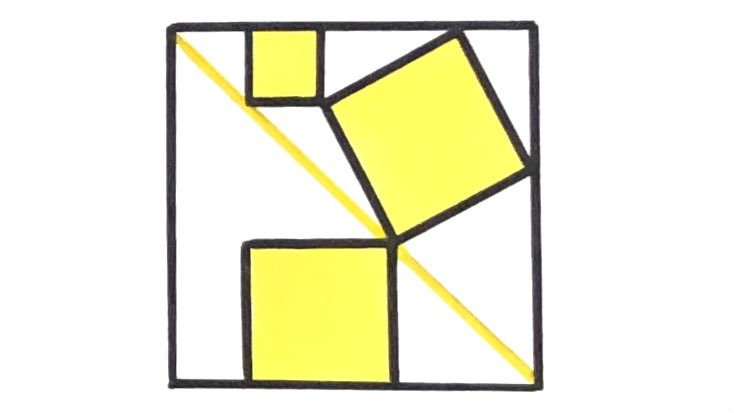
Four squares. What fraction is shaded?
Solution by Pythagoras' Theorem
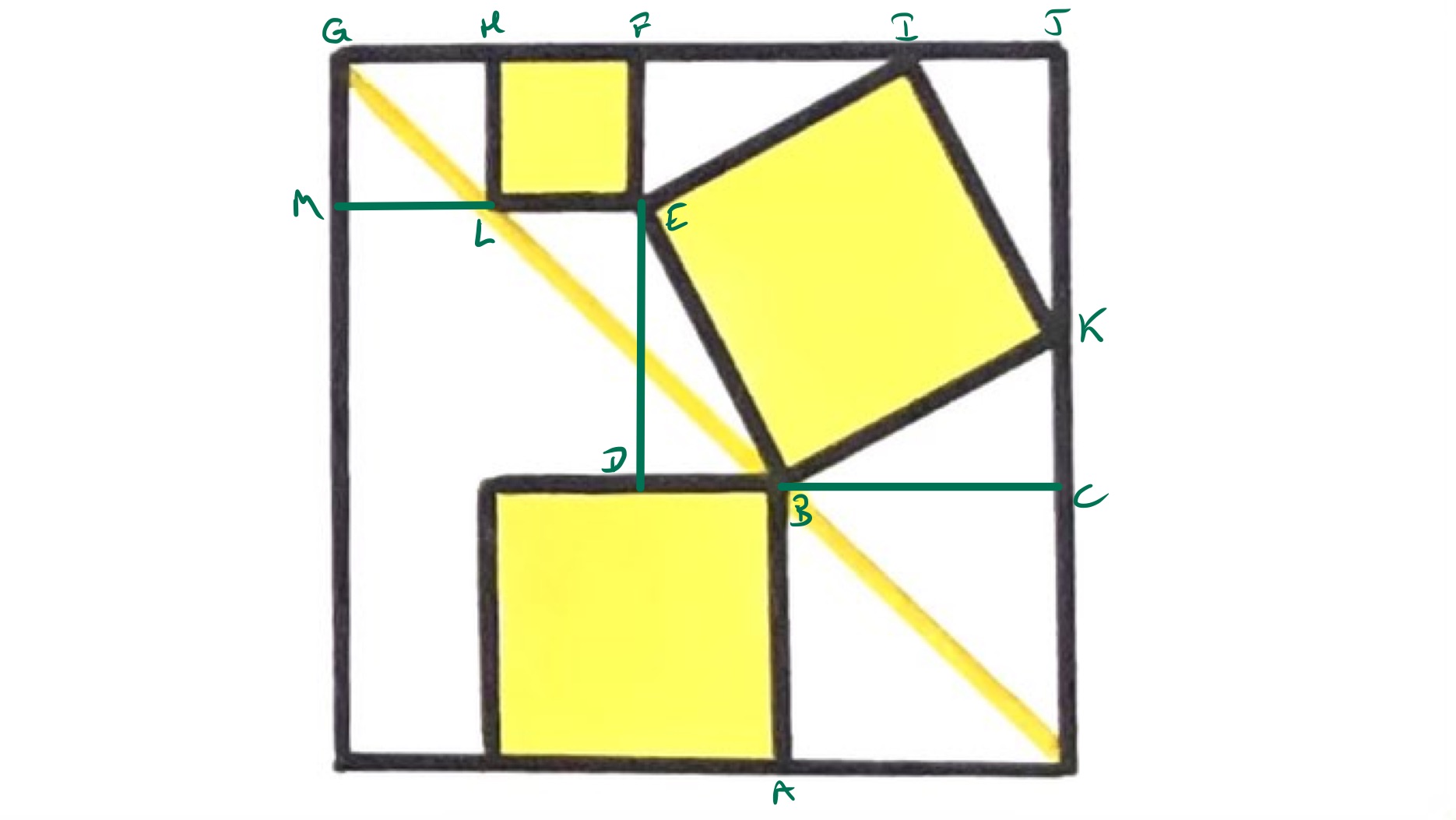
With the points labelled as in the above diagram, as the yellow line is a diagonal of the square, the lengths of and are the same. Similarly, and have the same length. The symmetry of the square , and the tilted square , shows that the line segments , , and all have the same length.
Now let be the length of and of . Reading across the top of the outer square, its width is . Reading up the middle, the height is . As it is a square, these are equal showing that . The width of the outer square is then so its area is .
Let be the length of . This is the hypotenuse of the right-angled triangle so applying Pythagoras' theorem shows that . The area of shaded region is therefore .
Therefore the fraction that is shaded is .