Notes
four squares vii solution
Solution to the Four Squares VII Puzzle
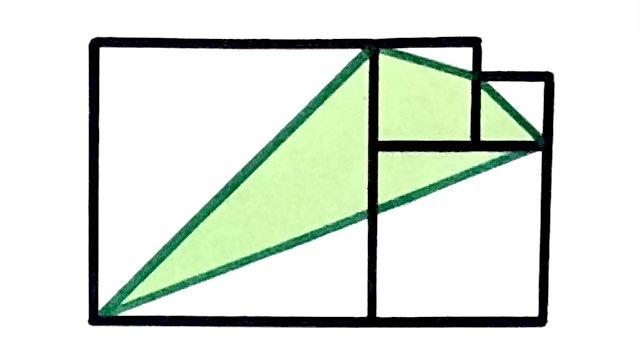
The green area is . What’s the total area of the four squares?
Solution by Calculation
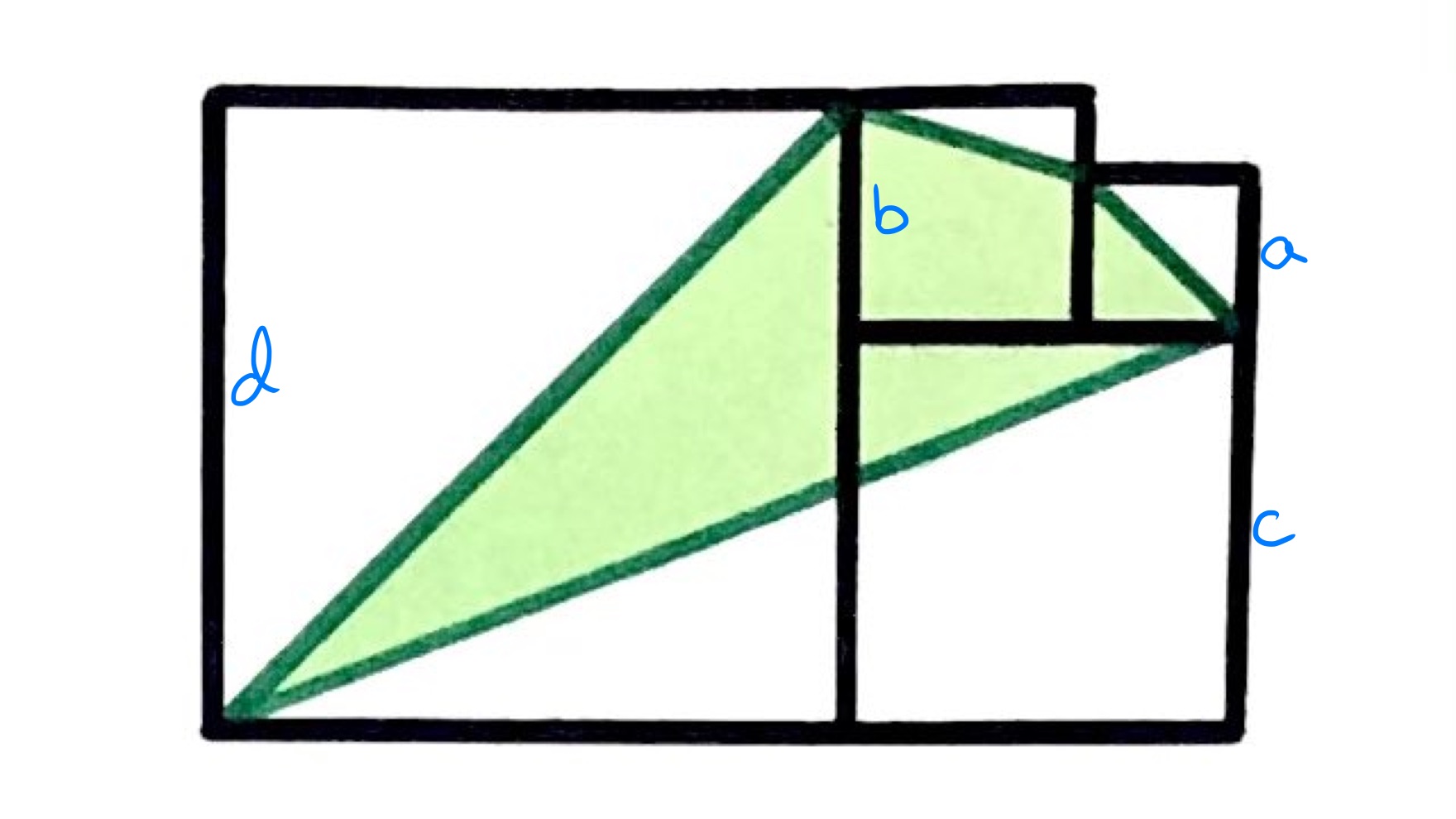
In the diagram above, , , , and are the side lengths of the squares in ascending order. We have and . Our goal is to compute given that the green area has area .
It is possible to rewrite everything in terms of and , but the expressions turn out to be more straightforward if instead everything is written in terms of and . This uses and .
This is because of the degenerate version of the parallelogram law (where the parallelogram lies on a straight line):
So the full area is:
The white area is easier to compute directly than the green as it is four right-angled triangles. It is:
We already know what is in terms of and , the other terms simplify as follows:
So the white area is . The green area is therefore and so the total area is:
Note: in the interest of completeness, it can be shown that the parts of the green region that lie in the square of side and of side have the same area as the lower white triangle in the largest square. However, unless and are in the correct proportion they do not fit as they are into that region but need further dissection. So although this can be used for a dissection method for finding the green area, it needs a little algebra to show that it works.
Solution by Invariance Principles
The part of this problem that can be varied is the relative sizes of the two small squares. The extremes for this are when the squares are the same size and when the smaller square is non-existant.
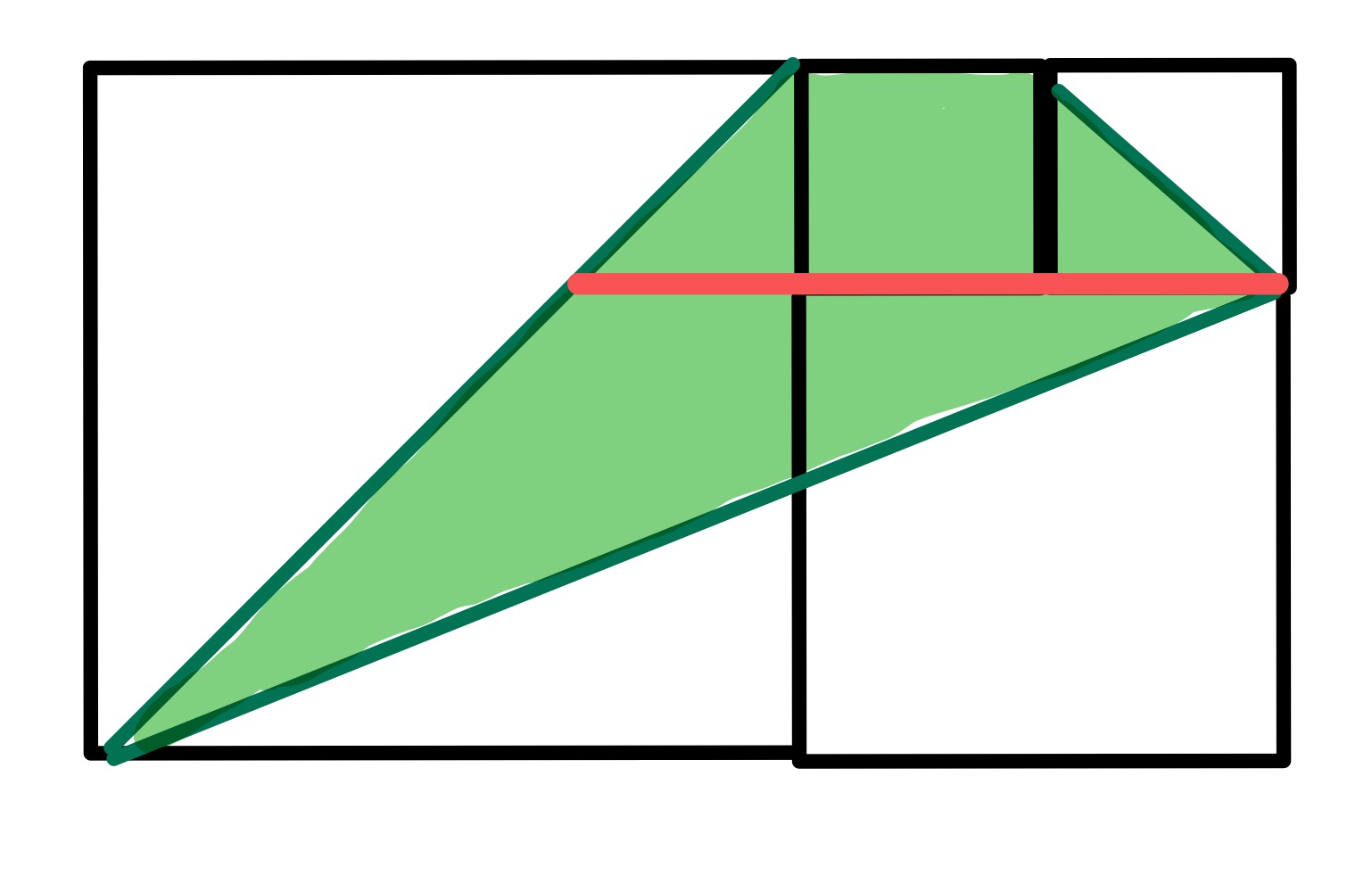
When the two are the same size, the relationships between the sizes are that , , and . The total area is therefore . The green area can be subdivided as above to show that its area is:
This shows that the total area is three times that of the green area, hence is .
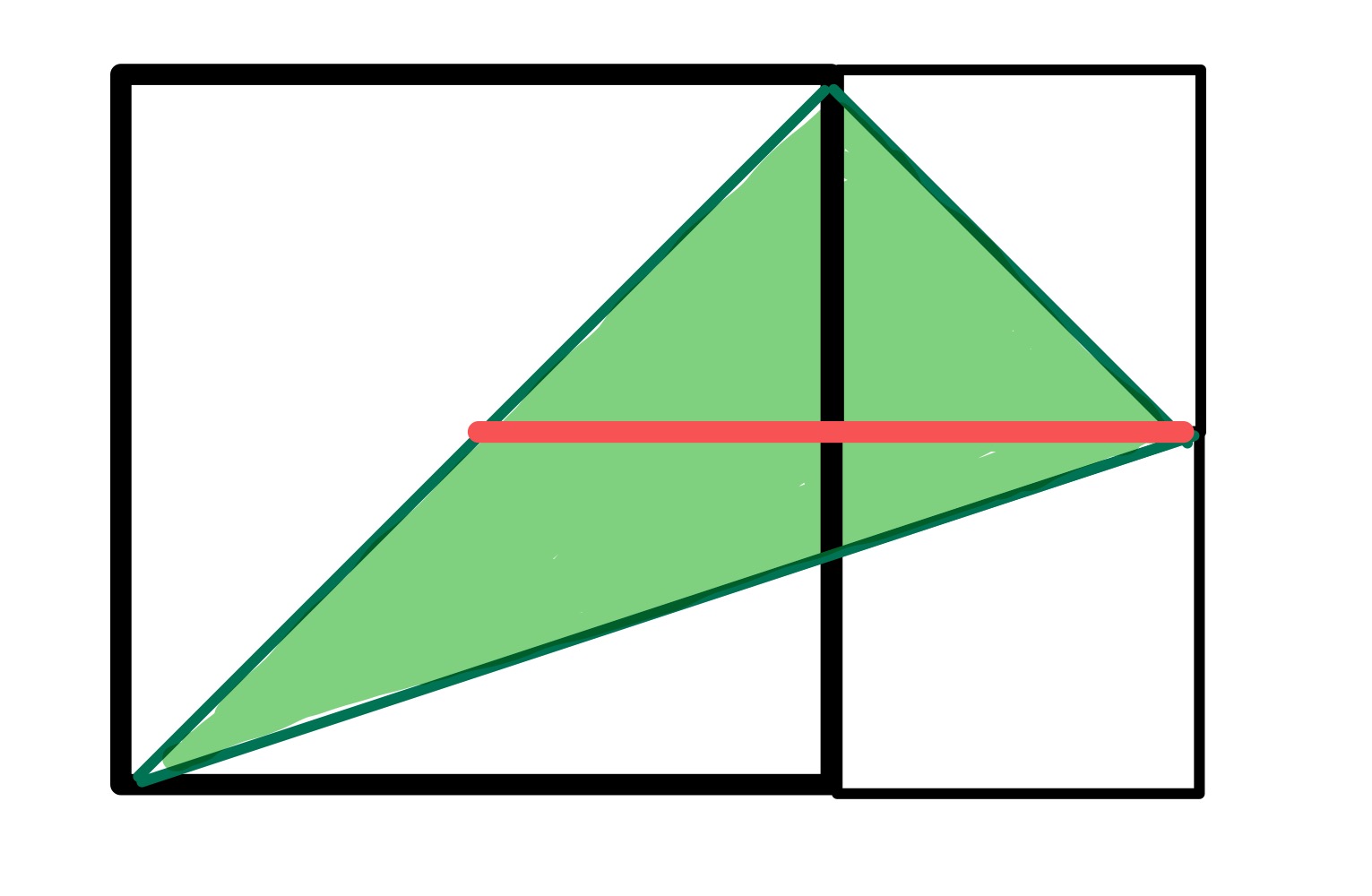
When the smallest square vanishes, the remaining squares have sizes and . The total area is therefore . The green area can be subdivided as above to show that its area is:
So, as before, as the green region has area , the total area is .