Notes
four squares v solution

Solution to the Four Squares V Puzzle

Solution by Symmetry and Dissection

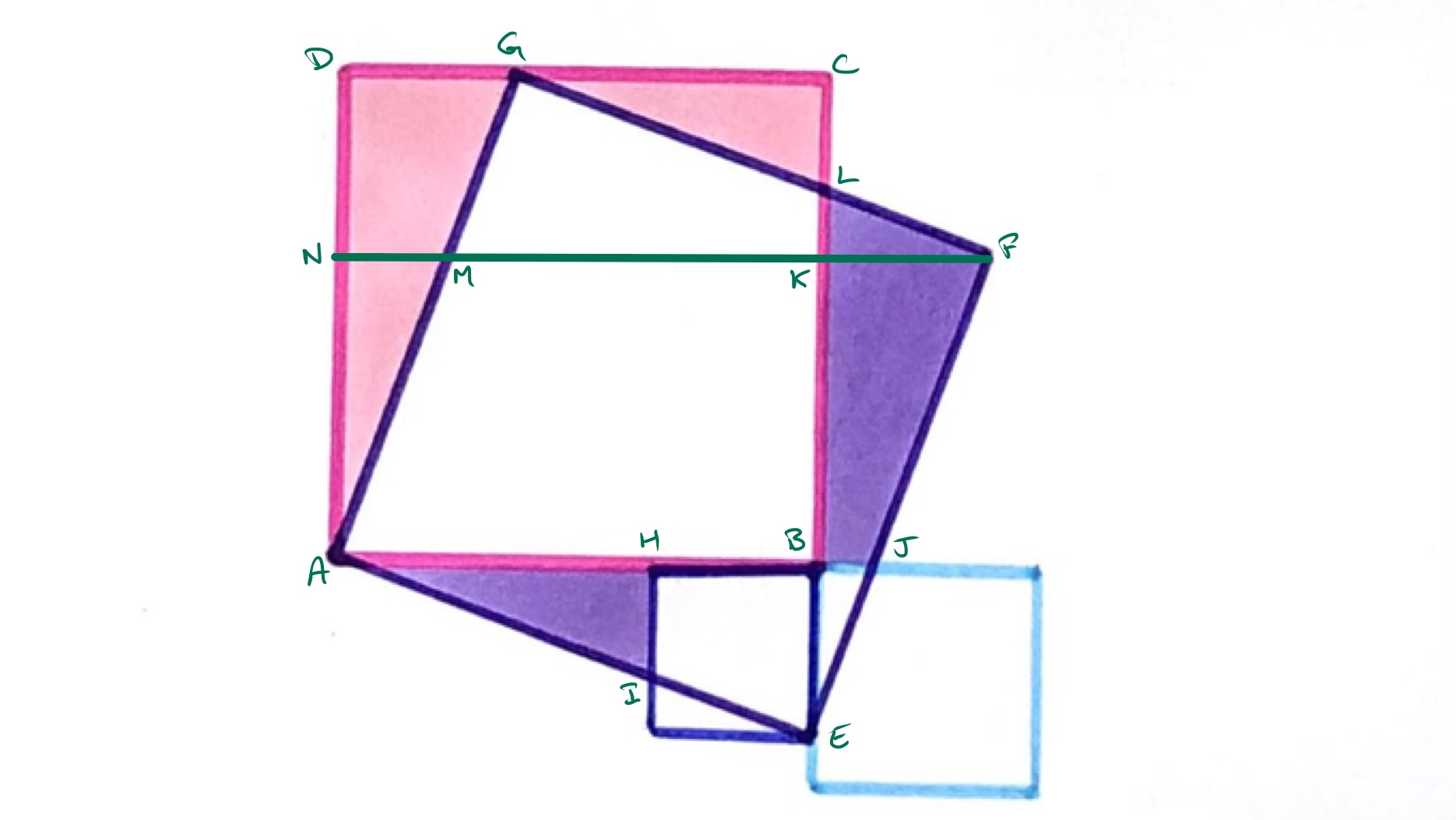
With the points labelled as above, consider rotating the diagram about the centre of the purple square by $90^\circ$ clockwise. This takes the line segment $M F$ to $L E$, and the side $A D$ rotates so that it overlaps with side $D C$, with $A$ rotating to $G$. The point $N$, as the intersection of $A D$ with the line through $M$ and $F$, therefore rotates to $C$. Comparing lengths, $N F$ and $C E$ are the same length, $N K$ and $C B$ are the same length, and therefore $K F$ and $B E$ are the same length.

Since angles $L \hat{F} K$ and $J \hat{E} B$ are the same, this establishes triangles $K F L$ and $B E J$ as congruent and therefore the area of quadrilateral $B J F L$ is the same as that of triangle $K E F$. This triangle is congruent to $D A G$, so the purple region $B J F L$ and has the same area as the pink region $D A G$.

This also establishes $K F$ as having the same length as $D G$. Since $H B$ and $B E$ also have the same length, this means that $G C$ and $A H$ have the same length. Therefore, triangles $G C L$ and $A H I$ are congruent and so have the same area.

Therefore the pink and purple regions have the same area.

Solution by Invariance Principle

Given that the solution doesn’t depend on the angle of the purple square, there is a configuration of the squares that makes it clear, as below.