Notes
four squares overlapping a circle solution
Four Squares Overlapping a Circle
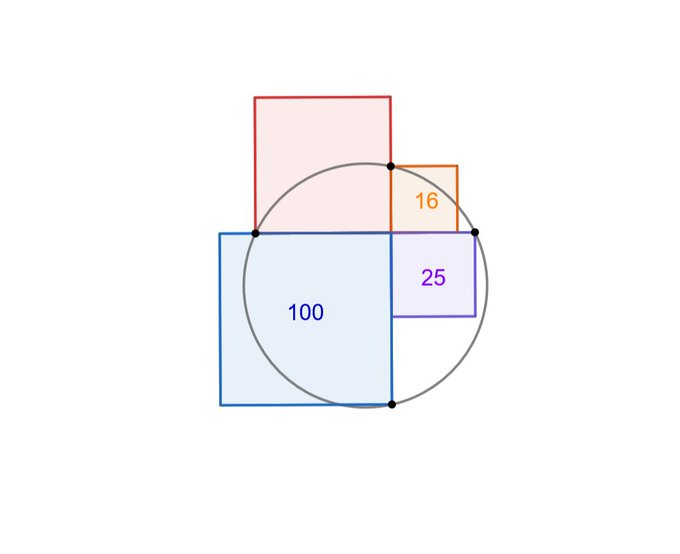
What’s the area of the circle?
Solution by the Intersecting Chords Theorem and Pythagoras' Theorem
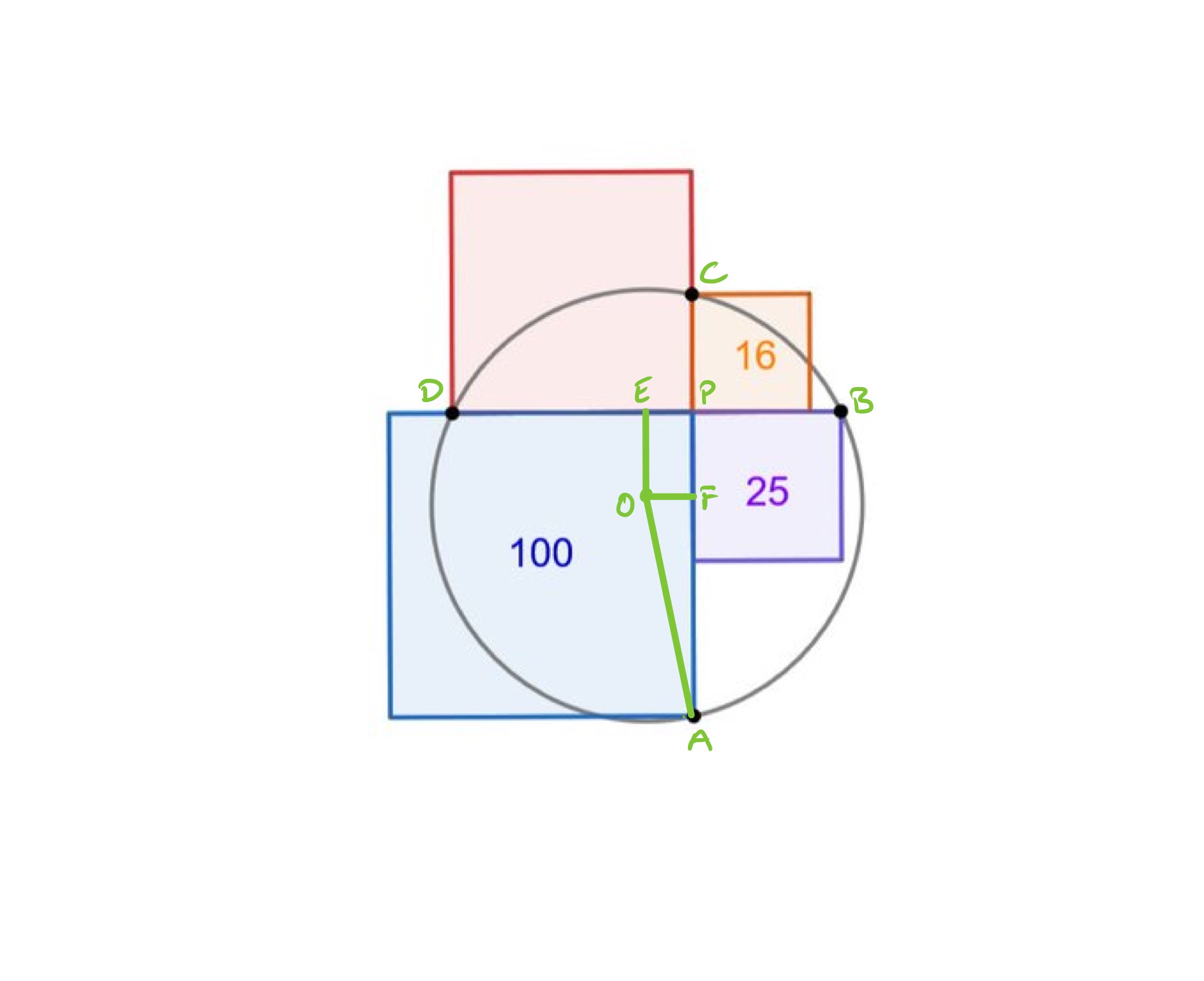
In the above diagram, point is the centre of the circle and and are so that angles and are right-angles. Since is a chord, is its midpoint and similarly is the midpoint of . From the areas of the squares, the following lengths can be deduced: has length , has length , and has length . Therefore has length .
The intersecting chords theorem says that the length of is given by . So has length and so has length . Let be the radius of the circle. Applying Pythagoras' theorem to triangle shows that . Therefore, the area of the circle is .