Notes
four squares iv solution

Solution to the Four Squares IV Puzzle

Solution by Angle at the Centre is Twice the Angle at the Circumference and Angle in a Semi-Circle

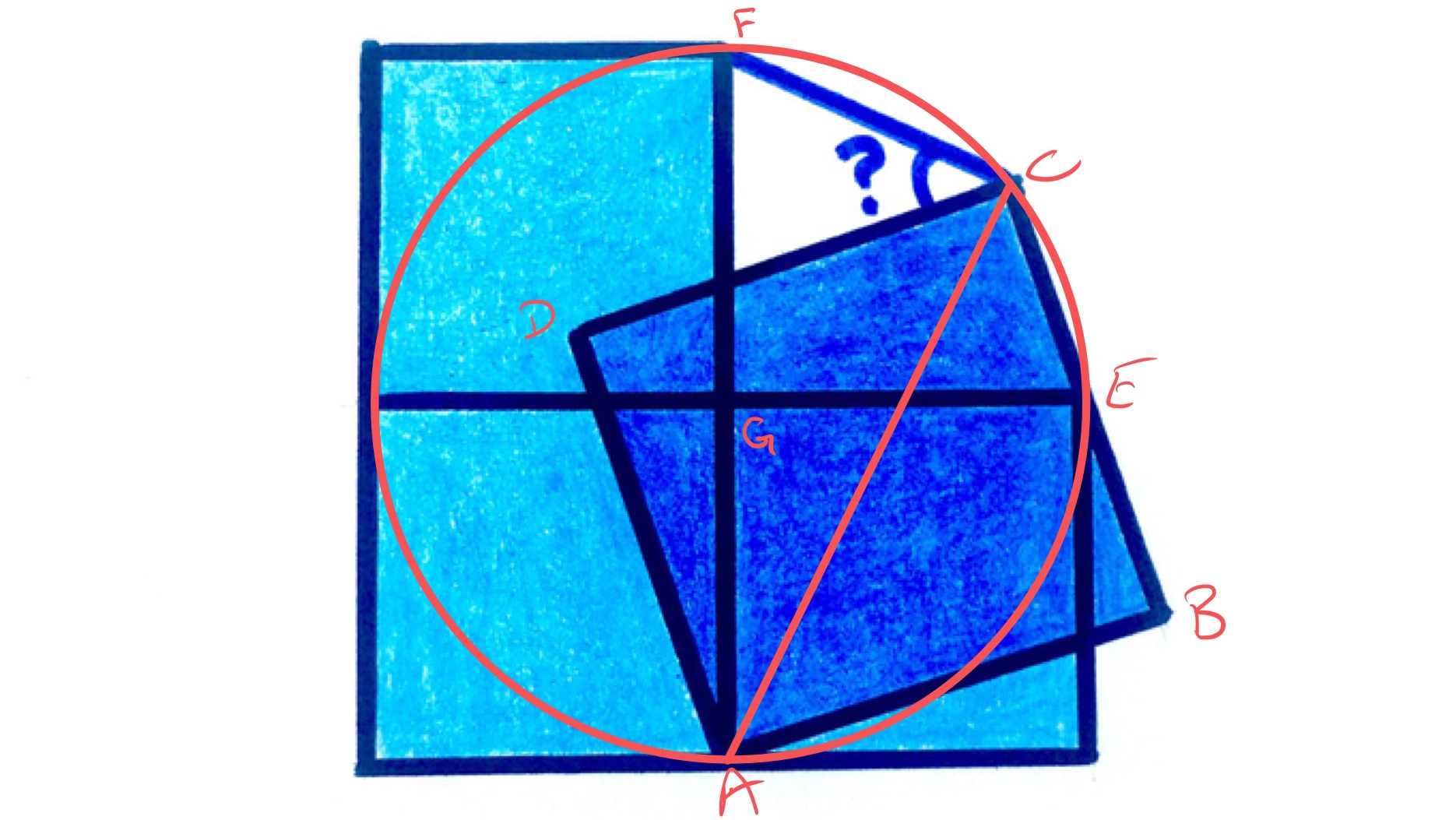
With the points labelled as in the above diagram, the circle is centred at $G$ and passes through the vertices $A$, $E$, and $F$ of the light blue squares.

As point $E$ lies on the line segment $C B$, angle $A \hat{C} E$ is $45^\circ$, while angle $A \hat{G} E$ is $90^\circ$. By the converse to the Angle at the Centre is Twice the Angle at the Circumference, this means that $C$ lies on the circle. Since $F A$ is a diameter of the circle, angle $F \hat{C} A$ is the angle in a semi-circle and so is $90^\circ$. Then as angle $D \hat{C} A$ is $45^\circ$, angle $F \hat{C} D$ is $45^\circ$.

Solution by the Invariance Principle

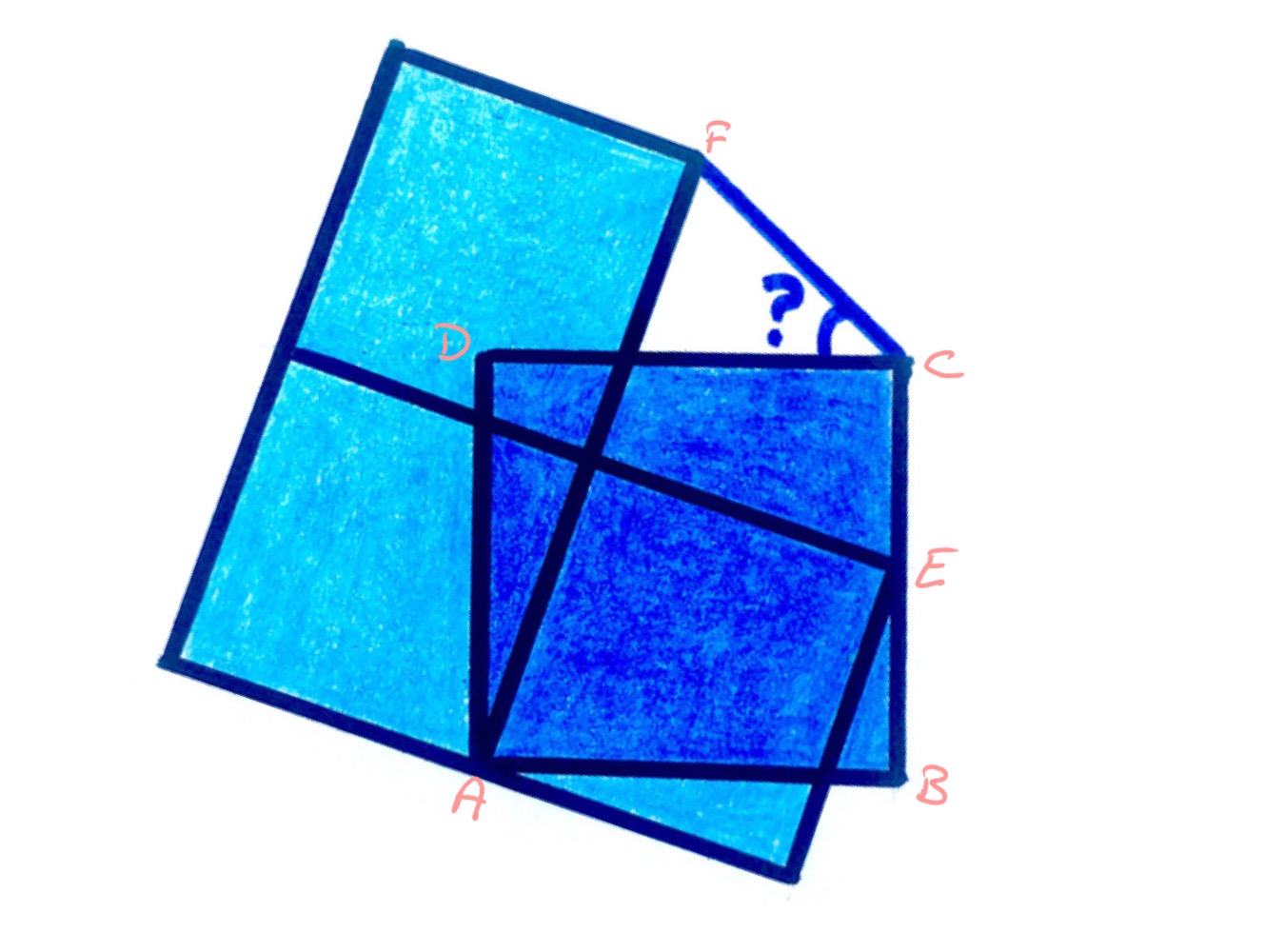
Consider the rotated diagram above and view the dark blue square, $A B C D$, as fixed. In this scenario, the point labelled $E$ is free to move on the line segment $B C$. As it does so, the point labelled $F$ also moves on a straight line (relative to the dark square). The extremes are when $E$ is at $B$ and at $C$ and are shown below. From this, $F$ moves on a line from $C$ at an angle of $45^\circ$ to the line segment $D C$.