Notes
four squares inside a rectangle solution
Solution to the Four Squares Inside a Rectangle Puzzle
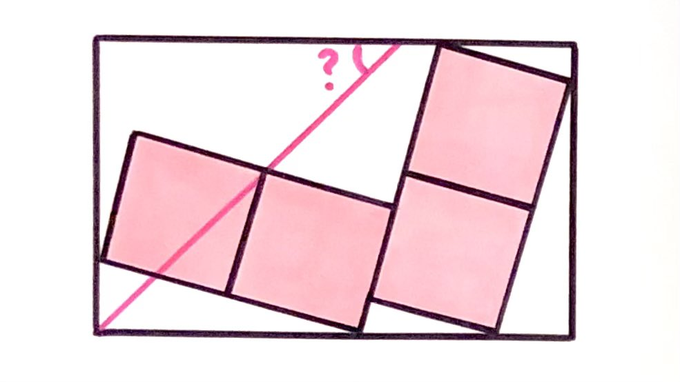
Four squares inside a rectangle. What’s the angle?
Solution by Angles in a triangle, Angles at a point on a straight line, and Angles in parallel lines
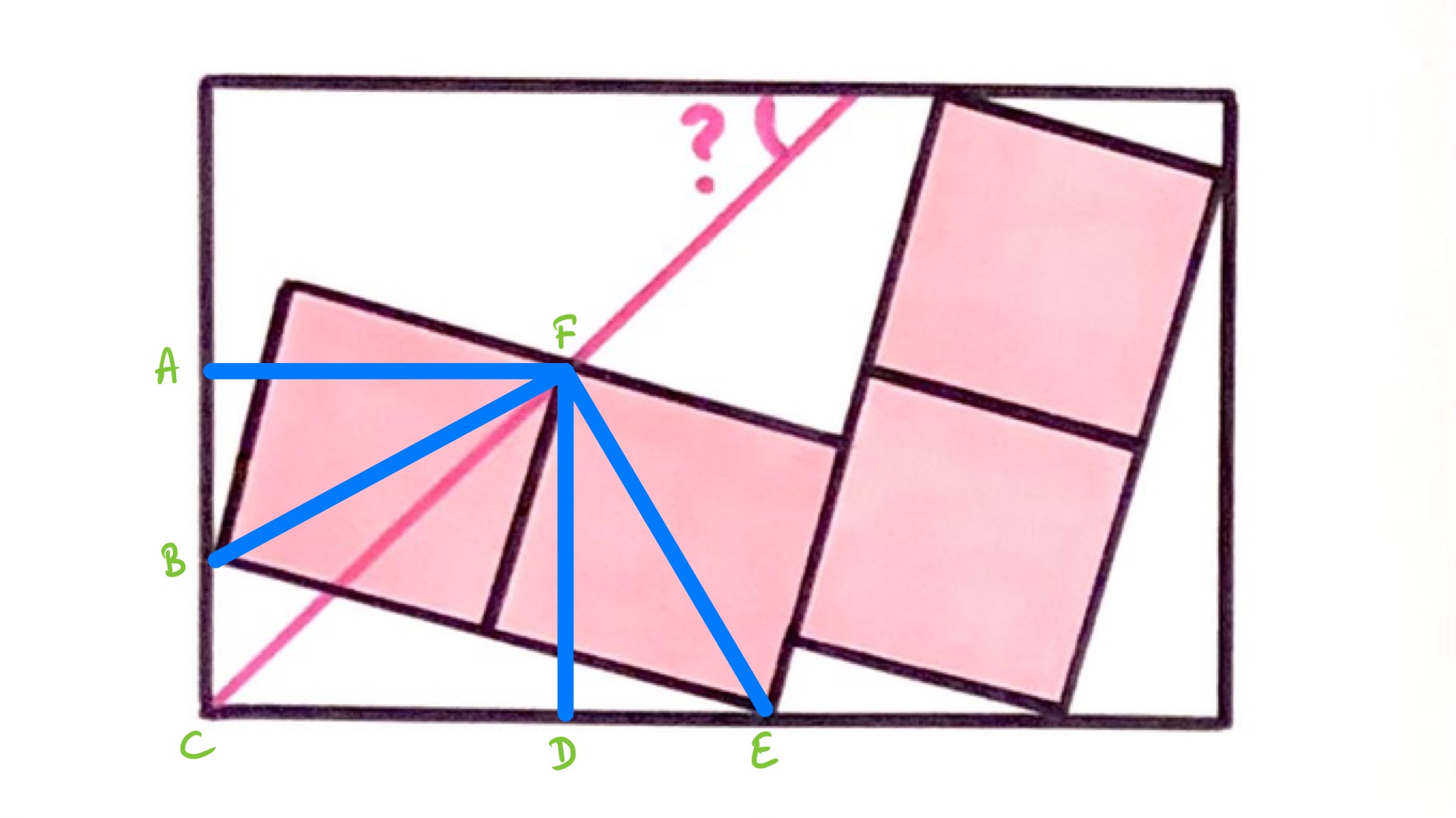
In the above diagram, is horizontally across from and is vertically below. So the quadrilateral has all four interior angles and so is a rectangle.
Considering angles at , and using that is a diagonal of the left-hand square, we have:
Over at , we have:
Then as triangle is a right-angled triangle:
Putting those together,
So triangles and are similar, and the lengths of and are the same, so they are congruent. This means that the lengths and are also the same and so the quadrilateral is actually a square.
The line is therefore at to and so the requested angle is also by angles in parallel lines.
Solution by Invariance Principle
The squares can be drawn at any angle inside the rectangle, so they can be drawn to align with the sides of the outer rectangle. This brings to and the left-hand square sits in the lower left corner of the rectangle. The line is then evidently at to the base of the rectangle.