Notes
four squares in a semi-circle solution
Solution to the Four Squares in a Semi-Circle Puzzle
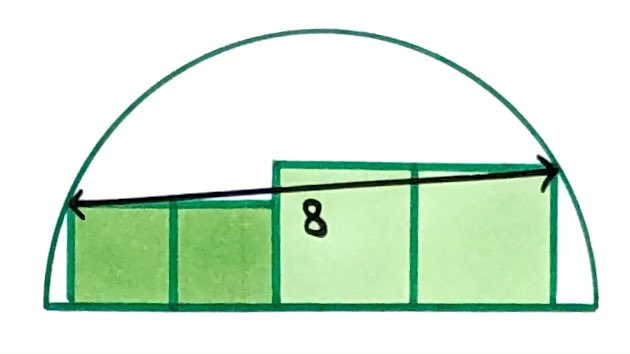
Four squares inside a semicircle. What’s the semicircle’s area?
Solution by Pythagoras' Theorem and similar triangles
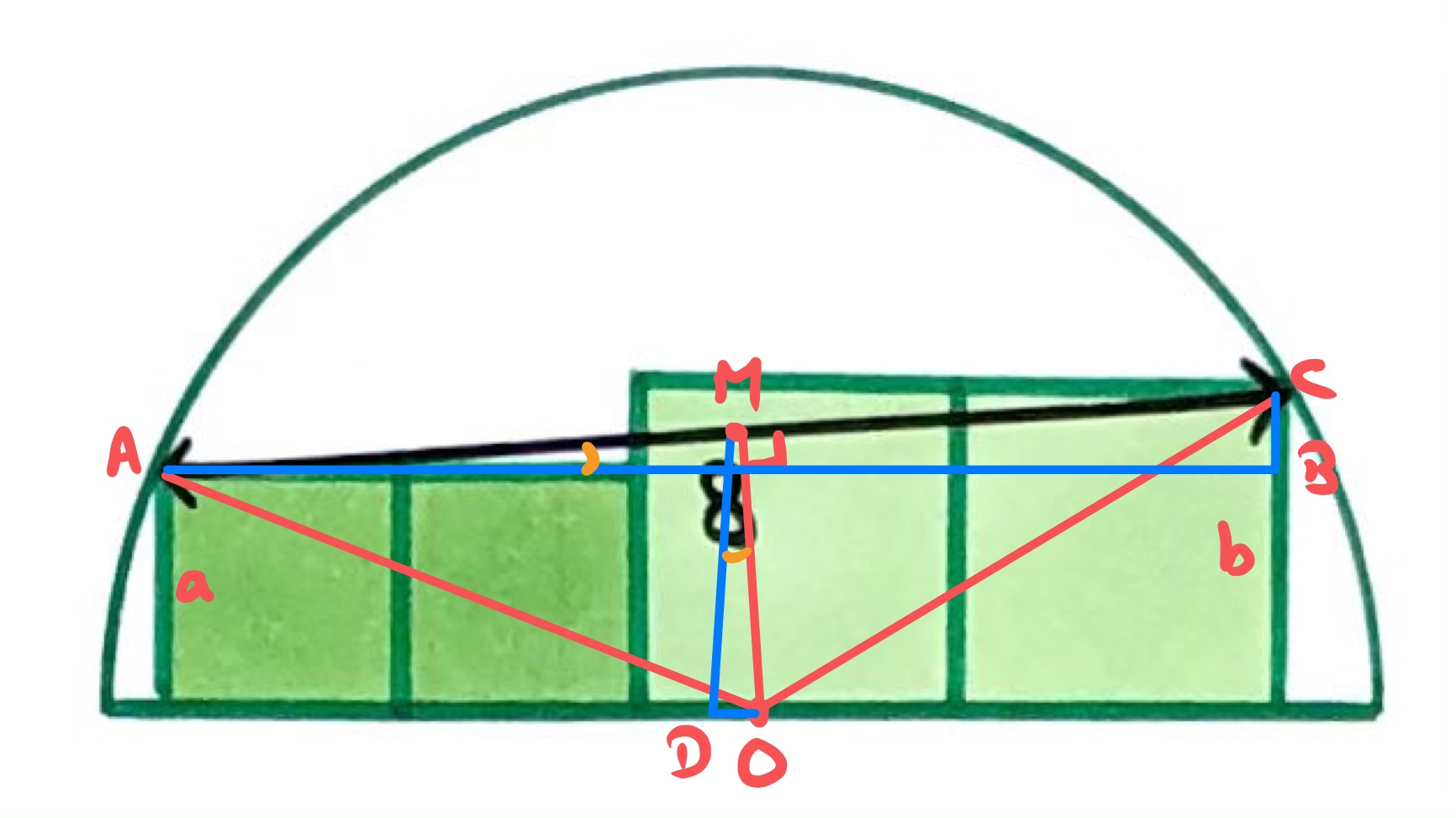
Let be the centre of the circle and the midpoint of the chord . Then and are radii of the circle and meets at a right-angle. As is the midpoint of , has length . To find a radius, we can use Pythagoras' Theorem on triangle once we have found the length of .
To find this, we start by noticing that triangles and are similar. So:
Let be the height of the left-hand boxes and the height of the right-hand boxes. Then . As is the midpoint of , its height above the diameter is and this is the length of . So the ratio is and so .
From Pythagoras’ Theorem, the radius satisfies
and so the area of the semi-circle is:
Solution by Invariance Principle
What can be varied here is the relative sizes of the two sets of squares. At each extreme, one pair of squares vanishes. Another useful configuration is when all four squares are the same size.
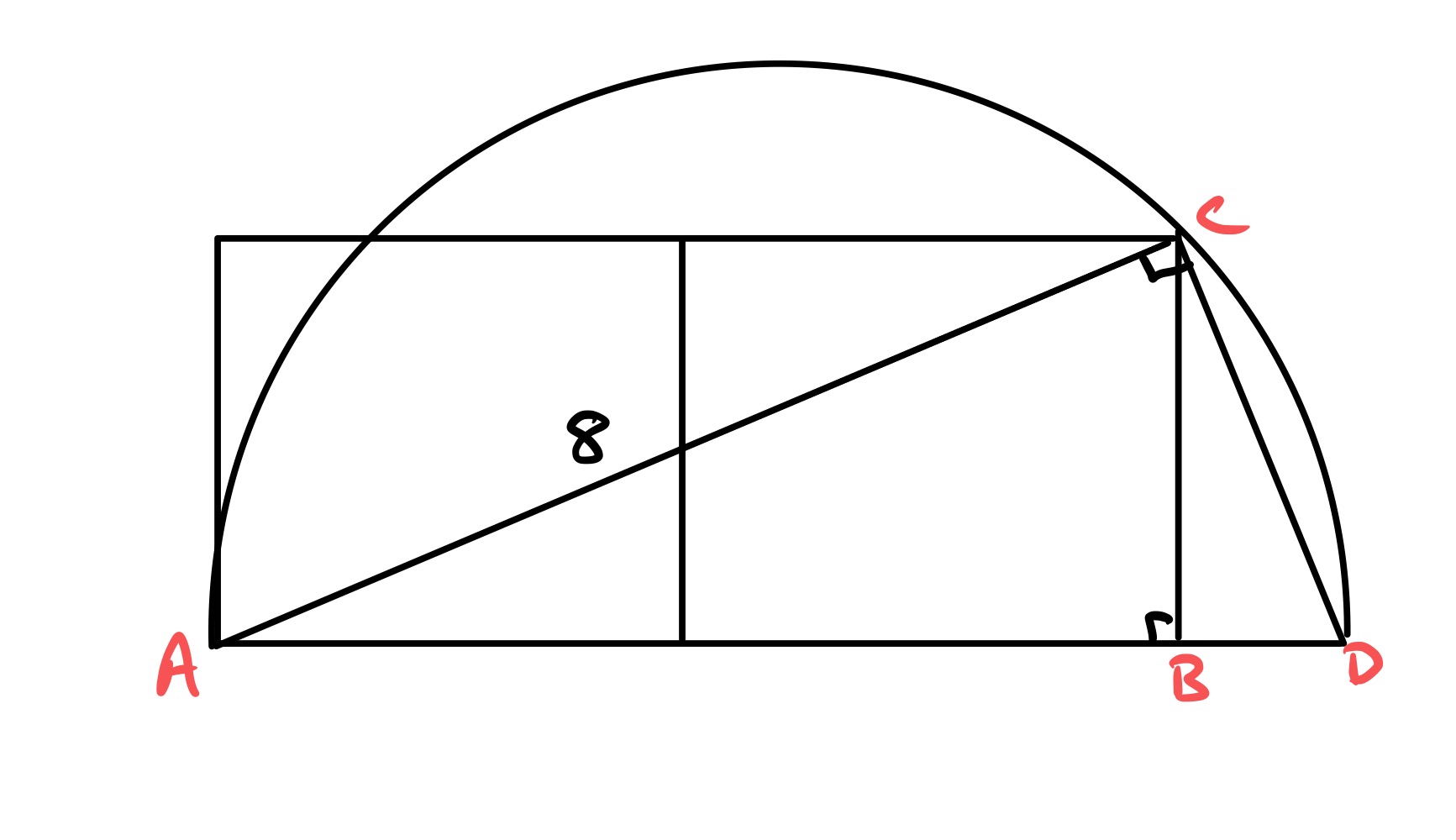
When two squares vanish, the length stretches across both remaining squares as the hypotenuse of the triangle in the above diagram. The remaining lengths, and are in the ratio . The triangle is similar to , with hypotenuse , so is half of , which is . Applying Pythagoras' Theorem to then , the diagonal of the semi-circle, is given by the square root of .
As the radius is half the diameter, its square is a quarter of the square of the diameter, and so is . The area of the semi-circle is therefore:
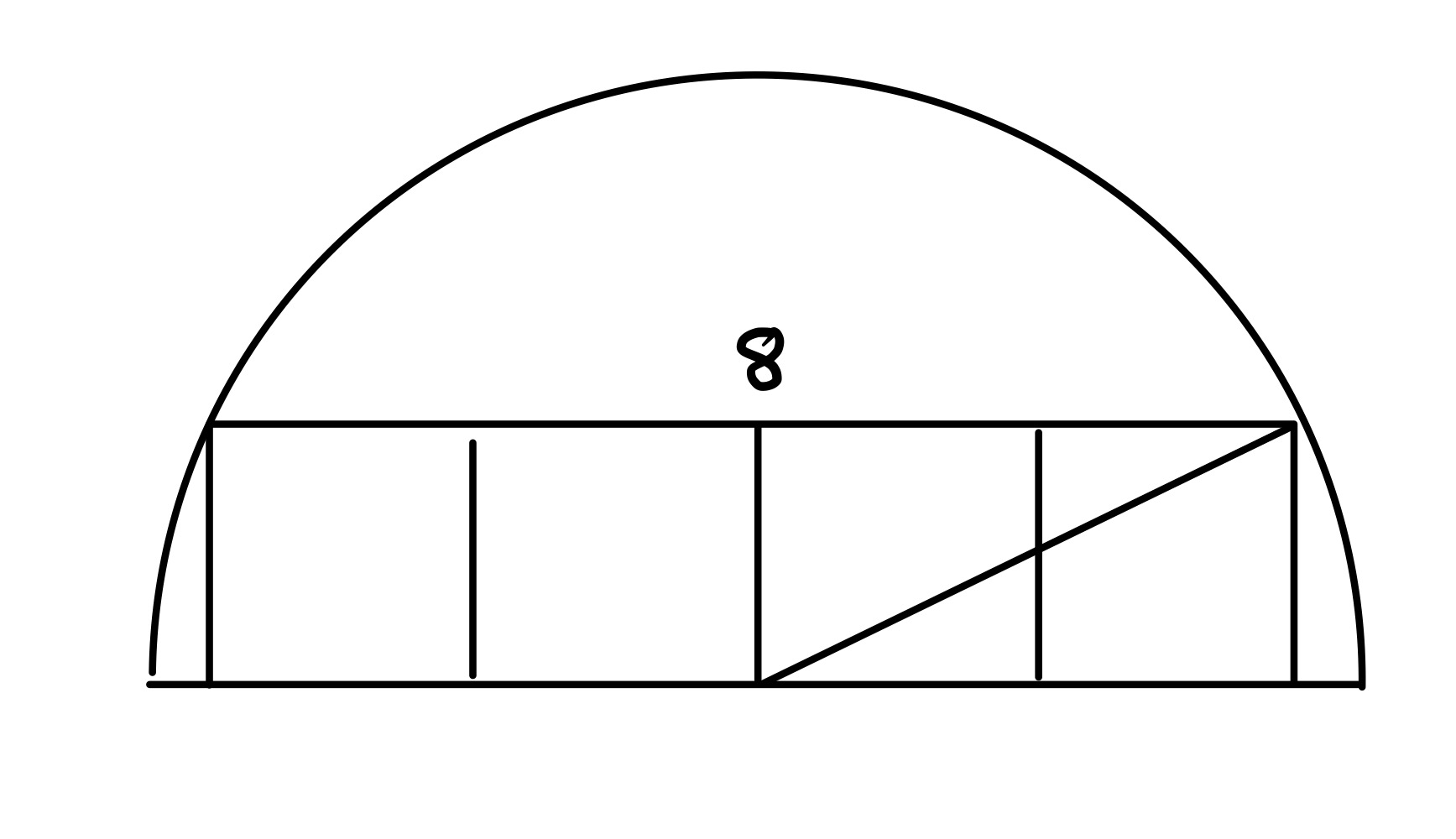
When all four squares are the same size, each must have side length of . The centre of the circle is now at the lower common vertex of the middle two squares, and the length of a radius is the diagonal of the rectangle comprising two of the squares. As each square has side length , Pythagoras' Theorem says that
This gives the area as